Kezdőlap


Feladat:	1197. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Orlay Imre , Tar Teréz
Füzet:	1963/május, 201 - 202. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Kör egyenlete, Kúpszeletek érintői, Feladat
Hivatkozás(ok):	Feladatok: 1962/október: 1197. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a két kör középpontja $O_{1}$ , ill. $O_{2}$ , egyik metszéspontjuk $P$ . (A másik metszéspont $P$ -nek $O_{1} O_{2}$ -re vett $P'$ tükörképe és ugyanez áll a $P$ -ben és $P'$ -ben húzott érintőkre, ezért az érintők $P$ -ben és $P'$ -ben egyenlő szögeket zárnak be; elég tehát a $P$ -beli szöget vizsgálnunk.) Az érintők merőlegesek a megfelelő sugárra, ezért köreink akkor és csak akkor metszik egymást merőlegesen, ha az $P O_{1}$ , $P O_{2}$ sugarak közti szög derékszög, más szóval ha az $O_{1} O_{2} P$ háromszög $P$ -nél derékszögű.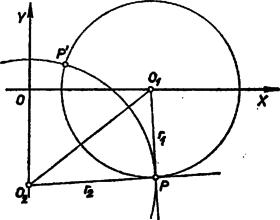

Ehhez elegendő megmutatnunk, hogy teljesül

\begin{matrix} P O_{1}^{2} + P O_{2}^{2} = O_{1} O_{2}^{2} . \end{matrix}

(3)

(1)-ből és (2)-ből teljes négyzetté való kiegészítéssel

\begin{matrix} {(x - a)}^{2} + y^{2} = a^{2} - b^{2}, \end{matrix}

ill.

\begin{matrix} x^{2} + {(y - c)}^{2} = b^{2} + c^{2}, \end{matrix}

innen látjuk, hogy

O_{1}

koordinátái

(a,0)

O_{2}

-éi

(0, c)

és a sugarak négyzete

r_{1}^{2} = a^{2} - b^{2}

, ill.

r_{2}^{2} = b^{2} + c^{2}

. Minthogy pedig

P O_{1} = r_{1}

és

P O_{2} = r_{2}

, ezért (3) bal oldala

\begin{matrix} r_{1}^{2} + r_{2}^{2} = a^{2} + c^{2}, \end{matrix}

másrészt (3) jobb oldalának értéke a koordinátákból ugyancsak ennyi, tehát az állítás igaz.
A (2) kör minden esetre létezik, mert

r_{2}^{2}

mindig pozitív, csak

b = c = 0

esetén

0

, ekkor a kör ponttá fajul el. Az (1) kör viszont csak

| a | > | b |

esetén;

| a | = | b |

esetén pedig ponttá zsugorodik. A két kör egybeesése csak

O_{1} = O_{2}

és

r_{1} = r_{2}

mellett következnék be, azaz ha

a = 0

c = 0

, ill.

b^{2} = 0

. Láttuk, hogy ebben az esetben mindkét kör ponttá fajul el.

Orlay Imre (Budapest, Budai Nagy A. Gimn. IV. o. t.)

II. megoldás. Megmutatjuk, hogy az

O_{1} P

O_{2} P

egyenesek

m_{1}

, ill.

m_{2}

iránytényezői egymásnak negatív reciprokai, más szóval, hogy szorzatukhoz

1

-et adva

0

-t kapunk. Ebből már következik, hogy

O_{1} P

és

O_{2} P

merőlegesek, és így ugyanez áll a

P

-ben húzott érintőkre is. Legyenek

P

koordinátái

(x_{0}, y_{0})

O_{1}

O_{2}

-nek az I. megoldásban felírt koordinátáival

\begin{matrix} m_{1} = \frac{y_{0}}{x_{0} - a}, m_{2} = \frac{y_{0} - c}{x_{0}}, és így \\ m_{1} m_{2} + 1 = \frac{y_{0} (y_{0} - c)}{(x_{0} - a) x_{0}} + 1 = \frac{x_{0}^{2} + y_{0}^{2} - a x_{0} - c y_{0}}{x_{0} (x_{0} - a)} . & (4) \end{matrix}

Ennek értéke valóban

0

, mert

(x_{0}, y_{0})

az (1)-et is, (2)-t is kielégíti, s így az azok összeadásával keletkező egyenletet is, tehát

\begin{matrix} 2 (x_{0}^{2} + y_{0}^{2} - a x_{0} - c y_{0}) = 0. \end{matrix}

Számításunkban feltételeztük, hogy

x_{0} \neq 0

és

x_{0} \neq a

. Ha

x_{0} = 0

, akkor (1)-ből

y_{0}^{2} + b^{2} = 0

, ami csak

b = 0

mellett lehetséges, és ekkor

y_{0} = 0

-ra vezet. Ekkor az

(x_{0}, y_{0})

pontban az (1) kör érintője az

Y

-tengely, a (2)-é az

X

-tengely, ezek merőlegesek, az állítás tehát helyes.‐ Ha

x_{0} = a

, akkor

P

O_{1}

-ben az

X

tengelyre állított merőlegesen van. Ekkor (1)-ből

y_{0}^{2} = a^{2} - b^{2} = r_{1}^{2} \neq 0

, és így(2)-ből

\begin{matrix} c = \frac{x_{0}^{2} - b^{2} + y_{0}^{2}}{2 y_{0}} = \frac{2 y_{0}^{2}}{2 y_{0}} = y_{0}, \end{matrix}

vagyis

P

O_{2}

-ben az

Y

-tengelyre állított merőlegesen van, az állítás ekkor is igaz.

Tar Teréz (Ócsa, Bolyai J. Gimn. IV. o. t.)

Megjegyzések. 1. Nem lényegesen különböző megoldást kapunk annak megmutatásával, hogy

P

rajta van az

O_{1} O_{2}

átmérő fölötti Thalész-körön.
2. Többen az iskolai tananyagon kívül álló ‐ néhol messze túlmenő ‐ fogalmak, tételek felhasználásával adtak további megoldást (pont hatványa körre; differenciál hányados). Tételekre való hivatkozásokat csak akkor fogadunk el, ha a versenyző azokat be is bizonyítja. Ez viszont az adott esetben messze vezetne.