Kezdőlap


Feladat:	1191. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bak Zsuzsanna , Corradi Gábor , Deák I. , Fazekas P. , Fejéregyházi S. , Földeáki Mária , Gerencsér L. , Gyárfás A. , Kelecsényi T. , Lakó F. , Lánc J. , Lehel Cs. , Lehel J. , Major J. , Makai E. , Mihályi Z. , Nárai Gy. , Pázmándi L. , Simon P. , Szidarovszky F. , Tamás Endre , Timár Gy. , Veres F.
Füzet:	1963/május, 194 - 198. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Szögfelező egyenes, Húrnégyszögek, Feladat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1191. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vizsgáljuk először azt az esetet, ha $D$ és $E$ az $A C$ ill. $A B$ félegyenesen van (1. ábra). Rajzoljunk egy a $B D = C E$ -vel egyenlő hosszú $P Q$ szakaszt és e fölé, a $P Q$ egyenes ugyanazon az oldalán egy a $B A D$ háromszöggel egybevágó $P A_{1} Q$ és egy a $C A E$ -vel egybevágó $P A_{2} Q$ háromszöget úgy, hogy az $A_{1}$ -ből, ill. $A_{2}$ -ből induló rövidebb oldal végpontja legyen $P$ , ha a két oldal nem egyenlő (2. ábra).

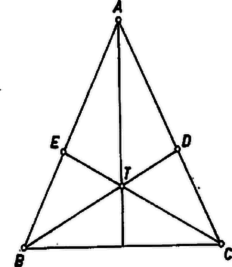1. ábra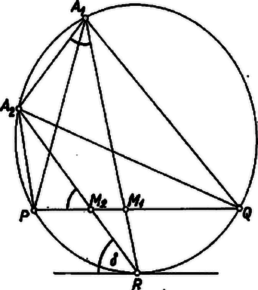

2. ábra

Ha a két háromszög egybeesik, ez azt jelenti, hogy vagy

D

C

-vel és

E

B

-vel egybeeesik (ebben az esetben nem teljesül szükségképpen a feladat állítása), vagy

A B = A C

és

A D = A E

. Ha

A_{1} P Q

és

A_{2} P Q

különböző háromszögek, akkor megmutatjuk, hogy

A_{1}

-ből, ill.

A_{2}

-ből induló szögfelezőiknek a szemközti oldalig terjedő szakaszai is különböző hosszúak. Ebből következni fog, hogy

A_{1}

és

A_{2}

nem lehet különböző, mert

B D

és

C E

D A B

szög felezőjén metszik egymást, s így, ha a két szakasz nem esik egybe, a

B A D

és

C A E

háromszögek

A

-ból induló szögfelezői nem lehetnek egyenlő hosszúak.
A szóban forgó két háromszög körülírt köre azonos, mert a

P Q

oldallal szemközti szögeik egyenlők és csúcsaik a

P Q

egyenes ugyanazon oldalán vannak. Az

A_{1}

-ból, ill.

A_{2}

-ből induló szögfelezőik az ezeket a csúcsokat nem tartalmazó

P Q

ív

R

felező pontján mennek át; messék a

P Q

oldalt az

M_{1}

ill.

M_{2}

Pontban. Feltehetjük, hogy a jelöléseket úgy választottuk, hogy a körön a pontok

R

P

A_{2}

A_{1}

sorrendben következnek. Ekkor

M_{2}

P

és

M_{1}

közt van, a háromszögek oldalaira tett kikötések folytán

M_{1}

is,

M_{2}

is a

P Q

szakasz

P

-felőli felére esik.
A kör

R

-ben húzott érintője párhuzamos

P Q

-val, s így az

R A_{2}

egyenessel bezárt

δ

hegyes szöge egyenlő a

P M_{2} A_{2}

szöggel. Másrészt

δ

R P A_{2}

íven nyugvó kerületi szög, s így egyenlő az

R A_{1} A_{2}

szöggel, mert

A_{1}

P

-t nem tartalmazó

A_{2} R

íven van. Így az

A_{1} A_{2} M_{2} M_{1}

négyszög húrnégyszög, mert

M_{2}

-nél levő külső szöge egyenlő a szemközti

A_{1}

csúcsnál levő belső szöggel. Ennélfogva a köréje írt kör

R

-ből húzható szelőire:

\begin{matrix} R M_{1} \cdot R A_{1} = R M_{2} \cdot R A_{2} . \end{matrix}

M_{1}

és

M_{2}

pontok sorrendjére tett megállapításból következik, hogy

R M_{1} < R M_{2}

, mert az

R M_{1} M_{2}

háromszög

M_{1}

-nél levő szöge tompaszög. Így a fenti egyenlőségből következik, hogy

\begin{matrix} R A_{1} > R A_{2} . \end{matrix}

Ezeket a szakaszokat az

M_{1}

, ill.

M_{2}

ponttal két részre bontva és az egyenlőtlenséget átrendezve

\begin{matrix} A_{1} M_{1} > A_{2} M_{2} + M_{2} R - M_{1} R > A_{2} M_{2}, \end{matrix}

vagyis a két szóban forgó szögfelező különböző. Láttuk azonban, hogy ez nem lehetséges, így a feladat állítása helyes.

D

és

E

A C

és

A B

szakasz

A

-n túli meghosszabbításán van (3. ábra), akkor

B

és

D

B A C

szög felezőjének egyik oldalán,

C

és

E

a másik oldalán van. Így, ha a

B D

és

C E

egyenes metszi ugyanabban a pontban a szögfelező egyenest, a metszéspont csak a

B D

és CE szakaszokon kívül lehet. Így a szögfelező az

A B D

és

A C E

háromszögek külső szögfelezője lehet, és ennek az

A

csúcstól a szemközti oldalig terjedő szakasza a két háromszögre nézve egyenlő (egybeesik). Rajzoljunk ismét a két háromszöggel egybevágó

A_{1} P Q

és

A_{2} P Q

háromszöget közös

P Q

alappal úgy, hogy

A_{1}

-et és

A_{2}

-t se a

P Q

egyenes, se a

P Q

szakasz felező merőlegese ne válassza el egymástól (4. ábra). A két háromszög köré írt kör itt is azonos, mert a

P Q

oldallal szemben levő szögek egyenlők, hiszen az

A B D

és

A C E

háromszögekben az

A

-nál levő szögek csúcsszögek. Az

A_{1} P Q

háromszög

A_{1}

-nél levő külső szögének a felezője merőleges a belső szögfelezőre, s így átmegy a fenti

R

-rel átellenes

R'

ponton (az

A_{1}

-et tartalmazó

P Q

ív felezőpontján). Ugyanitt megy át az

A_{2} P Q

háromszög

A_{2}

-nél levő külső szögének a felezője is. Ha a körön a pontok

R'

A_{1}

A_{2}

P

sorrendben következnek, akkor a szögfelezők

P Q

egyenesen levő

M_{1}

M_{2}

metszéspontjaira a

Q

P

M_{2}

M_{1}

sorrend áll fenn.
A kör

R'

-ben húzott érintője párhuzamos

P Q

-val, így az

R' M_{2}

-vel bezárt

δ

tompaszöge az

M_{1} M_{2} R'

szöggel egyenlő. Másrészt

δ

P

-t tartalmazó

R' A_{2}

íven nyugvó kerületi szög, s így egyenlő az

A_{2} A_{1} R'

szöggel, mert

A_{1}

P

-t nem tartalmazó

R' A_{2}

íven van. Az

A_{1} A_{2} M_{2} M_{1}

négyszög tehát itt is húrnégyszög, s így

\begin{matrix} R' A_{1} \cdot R' M_{1} = R' A_{2} \cdot R' M_{2} . \end{matrix}

R' M_{2} M_{1}

szög tompaszög, s így

R' M_{1} > R' M_{2}

, amiből a nyert egyenlőség folytán

\begin{matrix} R' A_{1} < R' A_{2} . \end{matrix}

Ebből következik, hogy

\begin{matrix} A_{1} M_{1} = R' M_{1} - R' A_{1} > R' M_{2} - R' A_{2} = A_{2} M_{2}, \end{matrix}

vagyis az

A_{1}

ill.

A_{2}

csúcstól a szemközti oldalig terjedő külső szögfelező szakaszok különbözők, ha

A_{1}

és

A_{2}

különböző. Ez nem lehetséges, kell tehát, hogy

A_{1}

és

A_{2}

egybe essék. Ekkor vagy

A B = A C

és

A D = A E

, vagy

A B = A E

és

A C = A D

. Utóbbi esetben

B D

és

C E

párhuzamos volna a

B A C

szög felező egyenesével, holott feltettük, hogy mindkettő metszi közös pontban ezt az egyenest. A feladat állítása tehát teljesül.

II. megoldás. A

B D

és

C E

szakaszok metszéspontját

T

-vel jelölve az

A B D

és

A C E

háromszögek

A

-nál levő szöge közös, a szemben levő

B D

és

C E

oldaluk egyenlő és

A T

(belső) szögfelezőjük ugyancsak közös (1. ábra). Az 1123. feladatban^{$^{*}$} láttuk, hogy a háromszög ebből az adathármasból egyértelműen megszerkeszthető, így a két háromszög egybevágó. A

B D

oldal

B

végpontjának a vele egyenlő

C E

oldal végpontjai közül nem felelhet meg

E

, mert ebből

A B = A E

és

A C = A D

következnék, és

T

határozatlan. Ezért

B

megfelelője

C

, így pedig

A B = A C

(és egyszersmind

A D = A E

, a

D

E

pontpár felcserélhető a

B

C

pontpárral).
Ha

D

és

E

mindegyike az

A C

, ill.

A B

oldal

A

-n túli meghosszabbításán van, akkor a feltevés második részét csak így vehetjük át: a

B D

és

C E

egyenesek

T

metszéspontja rajta van a

B A C

szögfelező egyenesén. Így

A D \neq A B

és

A E \neq A C

, különben ugyanis pl. az

A B D

háromszög egyenlő szárú, és

B D

párhuzamos a

B A D

szög külső szögének, a

B A C

szögnek felezőjével, tehát

T

nem jön létre. Feltehetjük, hogy

A D > A B

(3. ábra); így

T

nyilvánvalóan

B D

-nek

B

-n túli meghosszabbításán, vagyis a

B A C

szög fent használt felezőjén van, ezért fennáll

A E > A C

is. Ha ugyanis az állítást erre az esetre bebizonyítottuk, akkor az

A D < A B

(és

A E < A C

) eset erre visszavezethető úgy, hogy

B

C

D

E

helyett rendre

D

E

B

C

-t írunk.
Feltevéseink szerint az

A B D

és

A C E

háromszögek

A

-nál levő szögei egyenlők, mert csúcsszögek, velük a szemben levő

B D

és

C E

oldalak egyenlők, és az

A

-nál levő (közös) külső szögük felezőjének

A

és a szemben levő oldal egyenese közötti

A T

szakasza közös. A bizonyításnak az eredeti eset mintájára való befejezéséhez elég azt belátnunk, hogy a háromszöget egy oldala, a szemben levő szöge és e szög külső szöge felezőjének a csúcs és az oldal egyenese közti szakasza egyértelműen meghatározzák.
Valóban, az 1123. feladat I. megoldásának gondolatmenetét lényegében megismételve és az 5. ábra ugyanonnan átvett jelöléseivel az

A C B

szög külső szögének

C D'

felezője átmegy

K

-n, mert merőleges

C E

-re, így

B C K ∢ = B A K ∢ = D' B K ∢

, továbbá

B K C ∢ = D' K B ∢

K B C △ \sim K D' B △

K C : K B = K B : K D'

C D' = f

jelöléssel

K C (K C + f) = K B^{2}

, tehát az

A B

-ből és az

A C B

szögből kiadódó

k

-ban egyértelműen megszerkeszthető

K

és hozzá viszonyítva

C

helyzete (pl. az idézett megoldás mintájára szerkesztett

k_{1}

segédkör és a

G'

pont felhasználásával). ‐ Ezzel az állítást bebizonyítottuk.
Corradi Gábor (Győr, Czuczor G. Gimn. III. o. t.)

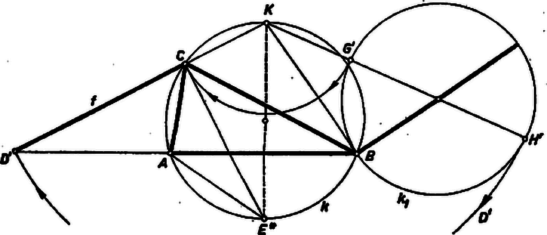5. ábra

Megjegyzés: A bebizonyított tétel egy speciális esete az, ha

B D

felezi a

C B A

szöget, ezért

T

a beírt kör középpontja, tehát

C E

is szögfelező, éspedig a

B C A

szögben. Eszerint bebizonyításaink magukban foglalják az 1159. feladat II. megoldása utáni 1. megjegyzésben^{$^{*}$} említett tétel fordított állításának bizonyítását. Ezt az állítást magában így is kimondhatjuk: ha egy háromszög két (belső) szögfelezője egyenlő, akkor a megfelezett szögek is egyenlők.
Az 1158. feladat példája (a két külső szögfelező egyenlősége) nem áll ellentétben feladatunk állításának második részével, mert a két egyenlő szögfelező szakasz egyikének végpontja egy belső szög szárán van, a másiké pedig az azt kiegészítő külső szög szárán.

^{$^{*}$}K.M.L. 24 (1962/5) 201. o.

^{$^{*}$}K.M.L. 25 (1962/11) 122. o.