Kezdőlap


Feladat:	1188. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gyárfás András , Pernek Tibor
Füzet:	1963/március, 128 - 130. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Derékszögű háromszögek geometriája, Kör egyenlete, Ellipszis egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1188. matematika feladat

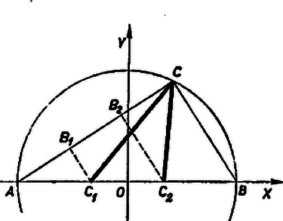
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az $A B C$ derékszögű háromszög $A B$ átfogójának harmadoló pontjai $C_{1}$ és $C_{2}$ , úgy, hogy $A C_{1} = C_{1} C_{2} = C_{2} B$ , ezek vetülete az $A C$ befogón $B_{1}$ , $B_{2}$ végül $B C = a$ , $C A = b$ , $A B = c$ . Nyilvánvaló, hogy $A B_{1} = B_{1} B_{2} = B_{2} C = b / 3$ , $C_{1} B_{1} = a / 3$ , $C_{2} B_{2} = 2 a / 3$ így a $C C_{1} B_{1}$ és $C C_{2} B_{2}$ derékszögű háromszögekből

\begin{matrix} C C_{1} + C C_{2} = \frac{1}{3} \sqrt[]{a^{2} + 4 b^{2}} + \frac{1}{3} \sqrt[]{4 a^{2} + b^{2}} = q . \end{matrix}

(1)

Ebből eltávolítjuk a négyzetgyököket. Négyzetre emeléssel

\begin{matrix} 5 a^{2} + 5 b^{2} + 2 \sqrt[]{(a^{2} + 4 b^{2}) (4 a^{2} + b^{2})} = 9 q^{2}, \end{matrix}

átrendezéssel és újabb négyzetre emeléssel

\begin{matrix} 16 (a^{4} + b^{4}) + 68 a^{2} b^{2} = 81 q^{4} - 90 q^{2} (a^{2} + b^{2}) + 25 (a^{4} + b^{4}) + 50 a^{2} b^{2}, \\ a^{4} + b^{4} - 2 a^{2} b^{2} - 10 q^{2} (a^{2} + b^{2}) + 9 q^{4} = 0. & (2) \end{matrix}

Itt az első három tag

a^{2} - b^{2}

-nek a négyzete, ami

\begin{matrix} a + b = p \end{matrix}

(3)

felhasználásával így alakítható át:

\begin{matrix} a^{4} + b^{4} - 2 a^{2} b^{2} = {(a^{2} - b^{2})}^{2} = {(a + b)}^{2} {(a - b)}^{2} = \\ = p^{2} (a^{2} + b^{2} - 2 a b) = p^{2} [{(a + b)}^{2} - 4 a b] = p^{4} - 4 p^{2} a b . \end{matrix}

Ezt (2)-be helyettesítve és a negyedik tagban

a^{2} + b^{2}

helyébe (3) alapján

p^{2} - 2 a b

-t írva

a b

-re nyerünk elsőfokú egyenletet:

\begin{matrix} p^{4} - 4 p^{2} a b + 20 q^{2} a b - 10 p^{2} q^{2} + 9 q^{4} = 0. \end{matrix}

Innen

\begin{matrix} a b = \frac{p^{4} - 10 p^{2} q^{2} + 9 q^{4}}{4 (p^{2} - 5 q^{2})} = \frac{(p^{2} - q^{2}) (p^{2} - 9 q^{2})}{4 (p^{2} - 5 q^{2})}, \end{matrix}

(4)

és a keresett átfogóra (3) alapján

\begin{matrix} c^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = p^{2} - \frac{(p^{2} - q^{2}) (p^{2} - 9 q^{2})}{2 (p^{2} - 5 q^{2})} = \\ = \frac{2 p^{4} - 10 q^{2} p^{2} - p^{4} + 10 p^{2} q^{2} - 9 q^{4}}{2 (p^{2} - 5 q^{2})}, \\ c^{2} = \frac{p^{4} - 9 q^{4}}{2 (p^{2} - 5 q^{2})} . & (5) \end{matrix}

Ha ez az érték pozitív, ennek a pozitív négyzetgyöke lehet csak az átfogó hossza. Miután azonban a (2) egyenlethez kétszeri négyzetre emelés útján jutottunk, lehetséges, hogy ezt olyan

a, b

értékek is kielégítik, amelyek (1)-et nem elégítik ki. Meg kell tehát vizsgálnunk, milyen

p, q

értékekre van (3), (4)-et kielégítő pozitív valós

a

és

b

, és teljesül-e azokra (1) is.
A (3), (4) összefüggések alapján

a

és

b

\begin{matrix} t^{2} - p t + \frac{(p^{2} - q^{2}) (p^{2} - 9 q^{2})}{4 (p^{2} - 5 q^{2})} = 0 \end{matrix}

(6)

egyenlet két gyöke. Ennek akkor és csak akkor van (valós) gyöke, ha diszkriminánsa nem negatív:

\begin{matrix} p^{2} - \frac{(p^{2} - q^{2}) (p^{2} - 9 q^{2})}{(p^{2} - 5 q^{2})} = \frac{q^{2} (5 p^{2} - 9 q^{2})}{p^{2} - 5 q^{2}} ≧ 0. \end{matrix}

(7)

A következők állapíthatók meg

p

és

q

nagyságviszonyáról: A

C C_{1} B_{1}

és

C C_{2} B_{2}

derékszögű háromszögekből egyrészt

\begin{matrix} C C_{1} < C B_{1} + B_{1} C_{1} = \frac{a + 2 b}{3}, ugyanígy C C_{2} < \frac{2 a + b}{3}, \end{matrix}

és ezekből összeadással

\begin{matrix} q < a + b = p . \end{matrix}

(8)

Másrészt

\begin{matrix} C C_{1} > C B_{1} = \frac{2 b}{3}, C C_{1} > C_{1} B_{1} = \frac{a}{3}, C C_{2} > \frac{b}{3}, C C_{2} > \frac{2 a}{3} \end{matrix}

összeadásával

\begin{matrix} 2 q > a + b = p . \end{matrix}

(9)

Ha ezek teljesülnek, (7) nevezője (9) szerint negatív, tehát számlálója nem lehet pozitív:

\begin{matrix} 5 p^{2} - 9 q^{2} ≦ 0, p ≦ q \sqrt[]{9 / 5} = q \sqrt[]{1, 8} . \end{matrix}

(10)

Ez a (9)-belinél kisebb felső korlátot szab meg a

p / q

hányadosra.
Ezek mellett a feltételek mellett az

a

-ra és

b

-re adódó értékek akkor pozitívak ‐ mivel összegük,

p

, pozitív ‐, ha szorzatuk, (4) jobb oldala is pozitív. Ez azonban teljesül, mert a számláló első tényezője (8) szerint pozitív, a második tényező és a nevező (10) szerint negatív. Ekkor a

c^{2}

-re nyert érték, mint két pozitív érték négyzetének összege, pozitív (ami a nyert kifejezésről közvetlenül is belátható). Ezek szerint akkor kapunk megoldást, ha

\begin{matrix} q < p < q \sqrt[]{1, 8} . \end{matrix}

(Látjuk, hogy nem lett volna elég a

c^{2}

-re kapott kifejezés pozitív voltát előírnunk. Abból ugyanis (8)-ra tekintettel

p < q \sqrt[]{3}

adódnék, és így lehetséges volna, hogy

c^{2}

pozitív, viszont

a

és

b

nem valósak.)

Pernek Tibor (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

Megjegyzés. Az (5) eredményhez koordináta-geometriai meggondolással is eljuthatunk. Vegyük

X

-tengelynek az

A B

egyenest, origónak az

A B

szakasz felezőpontját, így

A

C_{1}

C_{2}

B

abszcisszája rendre

- c / 2

- c / 6

c / 6

c / 2

. A keresett

c

-re abból kapunk egyenletet, hogy a derékszög

C

csúcsa három vonalon van rajta: az origó körül

c / 2

sugárral irt (Thalész-) körön, azon az ellipszisen, amelynek fókusza

C_{1}

és

C_{2}

, nagy tengelye

q

, és azon is, amelyiknek

A

és

B

a fókusza, nagy tengelye

p

. Így az ellipszisek kis tengelye fele hosszának négyzete

\begin{matrix} {(\frac{q}{2})}^{2} - {(\frac{c}{6})}^{2}, ill. {(\frac{p}{2})}^{2} - {(\frac{c}{2})}^{2} . \end{matrix}

Az ellipszisek

\begin{matrix} \frac{9 q^{2} - c^{2}}{36} x^{2} + \frac{q^{2}}{4} y^{2} = \frac{q^{2} (9 q^{2} - c^{2})}{144}, ill. \frac{p^{2} - c^{2}}{4} x^{2} + \frac{p^{2}}{4} y^{2} = \frac{p^{2} (p^{2} - c^{2})}{16} \end{matrix}

egyenletéből

x^{2}

-et és

y^{2}

-et kifejezve, majd a Thalész-kör

\begin{matrix} x^{2} + y^{2} = \frac{c^{2}}{4} \end{matrix}

egyenletébe helyettesítve

c^{2}

-re (hiányos) másodfokú egyenletet kapunk, annak 0-tól különböző gyöke azonos (5)-tel.

Gyárfás András (Budapest, Toldy F. g. IV. o. t.)