Kezdőlap


Feladat:	1187. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nárai György , Veres Ferenc
Füzet:	1963/március, 124 - 127. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Feladat
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1187. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Minden felbontásban 4 átló szerepel, mert az 5 háromszög 15 oldala közül 7 a hétszögnek is oldala, a maradó 8 oldalt átlók alkotják, és minden átló két háromszögnek oldala. Az átlók 8 végpontja csúcsa a hétszögnek, tehát legalább egy csúcsból legalább 2 átló indul; másrészt egy csúcsból legfeljebb 4 átló húzható.
Hétszögünk szabályos voltára tekintettel bármely két felbontást azonosnak tekintünk, ha a hétszög valamely szimmetriájával egymásba átvihetők. Nevezzük egy felbontásban 4-ágú csomónak (ill. 3-, 2-, 1-, 0-ágú csomónak) a hétszög minden olyan csúcsát, melyből pontosan 4 (ill. 3, 2, 1, 0) a felbontásban felhasznált átló indul ki, és képezzük a felbontásokat legtöbb ágú csomójuk csökkenő rendjében.
Egy csúcsból minden átlót meghúzva ‐ vagyis 4-ágú csomót képezve ‐ egy kívánt felbontást kapunk, és elforgatástól eltekintve csak egy ilyen van (1. ábra).
Ha egy csomót 3-ágúvá akarunk kialakítani (ilyenkor természetesen nincs 4-ágú csomó), akkor a képezést kétféleképpen kezdhetjük: a kiszemelt csúcsból kiinduló 4 átló közül vagy egyik szélsőt nem használjuk (vagyis a második csúcsba vezető, rövidebb átlót, 2. ábra), vagy egyik belsőt (a harmadik csúcsba vezetőt, a hosszabbat, 3. ábra). Ezzel azonban a felbontás meg is van határozva, ez a 3 átló a hétszöget 3 háromszögre és 1 négyszögre bontja, és a négyszög átlói közül csak azt használhatjuk a kettévágáshoz, amelynek a 3-ágú csomó nem végpontja (az ábrákon szaggatva). Így a felbontásban egy, ill. két 2-ágú csomó keletkezik.

Végül ha még 3-ágú csomót sem engedünk meg, akkor bármelyik kétágú csomóból kifutó két átló a hétszögnek két szomszédos csúcsába vezet. Ugyanis az ellentétes esetben a hétszögnek a köztük levő része négyszög, vagy ötszög, ennek felbontására a két átló szabad végpontjait összekötő átlót harmadik vágás gyanánt fel kell használnunk. Így a még egyben maradt négyszög két szomszédos csúcsa máris 2-ágú csomó, ezért bármelyik átlója menti kettévágásával 3-ágú csomó keletkezik. Mármost az elsőnek megválasztott 2-ágú csomóból akár a 2 hosszabb átlót indítjuk, akár 1 hosszút és a szomszédos rövidet, továbbfejlesztéssel mindig a 4. ábra felbontásához jutunk.
Ezek szerint a felbontások száma 4.

Veres Ferenc (Miskolc, Kilián Gy. g. III. o. t.)

Megjegyzés. Sokan a tengelyes tükrözéssel és forgatással egymásba átvihető felbontásokat különbözőknek tekintették, és így 42 felbontást adtak meg eredmény gyanánt. Valóban, így a 2. és 3. ábra egyenként

2 \cdot 7

felbontást ad, az 1. és 4. ábra pedig 7-et-7-et, ezek ugyanis tengelyesen szimmetrikusak.

II. megoldás. Először egy tetszés szerinti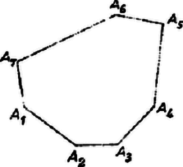

\begin{matrix} A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{7} \end{matrix}

konvex hétszög felbontásainak számát állapítjuk meg (5. ábra) és ezt

F_{7}

-tel jelöljük. Csoportosítsuk a felbontásokat aszerint, hogy az

A_{1} A_{2}

oldalt tartalmazó háromszög harmadik csúcsa

A_{3}

A_{4}

A_{5}

A_{6}

, ill.

A_{7}

5. ábra

Az első esetben az

A_{1} A_{2} A_{3}

háromszög mellett az

A_{1} A_{3} A_{4} A_{5} A_{6} A_{7}

konvex hatszög keletkezik, ilyen felbontás tehát annyi van, ahányféleképpen egy konvex hatszöget lehet egymást nem metsző átlókkal háromszögekre bontani. Jelöljük ezt a számot

F_{6}

-tal.
Első háromszögünknek

A_{1} A_{2} A_{4}

-et véve, ennek egyik oldalán az

A_{2} A_{3} A_{4}

háromszög keletkezik, másik oldalán az

A_{1} A_{4} A_{5} A_{6} A_{7}

konvex ötszög. Ilyen felbontás tehát

F_{5}

számú van, így jelölve egy ötszög megfelelő felbontásainak számát.
Az

A_{1} A_{2} A_{5}

háromszögből kiindulva további feladatunk az

A_{2} A_{3} A_{4} A_{5}

és

A_{1} A_{5} A_{6} A_{7}

konvex négyszögek felbontása. Mindegyiké külön

F_{4} = 2

-féleképpen lehetséges. És mivel az első négyszög bármelyik felbontása a másodiknak bármelyik felbontásával összekapcsolható, azért az

A_{1} A_{2} A_{5}

háromszöget tartalmazó felbontások száma

F_{4} \cdot F_{4} = 4

.
Az

A_{1} A_{2} A_{6}

és

A_{1} A_{2} A_{7}

háromszögekből kiindulva a második, ill. első vizsgált esettől csak betűzésben különböző esetre jutunk.
Nyilvánvaló, hogy így minden felbontást pontosan egyszer számbavettünk, ezért

\begin{matrix} F_{7} = F_{6} + F_{5} + F_{4} \cdot F_{4} + F_{5} + F_{6} . \end{matrix}

(1)

Ezzel a feladatot visszavezettük

F_{6}

és

F_{5}

megállapítására. Ezt a fenti meggondolásnak egyre kisebb oldalszám mellett való megismétlésével kaphatjuk. Nyilvánvaló azonban, hogy meggondolásunk nagyobb oldalszám mellett is használható és eredménye így írható:

\begin{matrix} F_{n} = F_{n - 1} + F_{3} \cdot F_{n - 2} + F_{4} \cdot F_{n - 3} + ... + F_{n - 3} \cdot F_{4} + F_{n - 2} \cdot F_{3} + F_{n - 1} . \end{matrix}

(2)

A második tagba és az utolsó előttibe is tényezőül felvett

F_{3}

értéke természetesen 1, ezt a kiegészítést a többi közbülső tag szerkezetével való azonosság kidomborítása végett alkalmaztuk.
Minthogy

F_{4} = 2

, azért képletünkkel

\begin{matrix} F_{5} = F_{4} + F_{3} \cdot F_{3} + F_{4} = 5, \\ F_{6} = F_{5} + F_{4} \cdot F_{3} + F_{3} \cdot F_{4} + F_{5} = 14, \end{matrix}

és így (1)-ből

F_{7} = 42

.
Szabályos 7-szög (általában

n

-szög) bármelyik csúcsa bármelyik másiknak a helyére forgatható úgy, hogy ugyanakkor minden más csúcs is egy másik csúcs helyére jut, így a fenti 42 felbontás 7-esével azonos, tehát legfeljebb 6 különböző. Köztük még vannak tükrös párok.
Az

A_{5}

csúcson átmenő szimmetriatengelyre tükrös megoldásban szerepel az

A_{1} A_{2} A_{5}

egyenlő szárú háromszög, a két oldalán létrejövő négyszögek egyikét

F_{4}

-féleképpen bonthatjuk, ez a másik felbontását is megadja, tehát a tengelyesen tükrös felbontások száma 2. A nem egybevágó felbontások száma

6 - 2 = 4

.
Nárai György (Budapest, Bem J. g. IV. o. t.)

Megjegyzések. 1. Általában a tengelyesen tükrös, nem egybevágó felbontások száma a szabályos (

2 n + 1

)-szög esetén a fentihez hasonlóan

F_{n + 1}

, ‐ természetesen

n ≧ 2

. Általános megállapítások kimondásában azonban óvatosságot ajánlunk versenyzőinknek. Ez a szám a szabályos

2 n

-szög esetében csupán

F_{n + 1} / 2

. Ugyanis az előbbi egyenlő szárú háromszög helyén egy leghosszabb átló, szimmetriatengely áll, és erre merőleges szimmetriatengely is van. ‐ Az sem helyes, hogy bármely szabályos

n

-szög egymásba forgással át nem vihető felbontásainak száma

F_{n} / n

. Ez a hányados mindjárt

n = 6

, 8, 9 esetén nem is egész szám. Ha ugyanis

n

nem primszám, akkor lehetségesek önmagukkal fedésbe forgatható felbontások, pl. a szabályos hatszögnek az a felbontása, melyben három egymáshoz a végpontjukkal csatlakozó rövidebb átlót használunk fel (6. ábra).

6. ábra

2. Az alábbiakban

F_{n}

-re a (2)-nél egyszerűbb kifejezést állítunk elő. A (2) jobb oldalán álló

F_{3} \cdot F_{n - 2}

F_{4} \cdot F_{n - 3}

...

F_{n - 2} \cdot F_{3}

szorzatok ‐ általános alakjuk

F_{k} \cdot F_{n - k + 1}

, ahol

3 ≦ k ≦ n - 2

‐ sorra a következő kérdésre is megadják a választ: a

B_{1} B_{2} ... B_{n - 1} = B

konvex

(n - 1)

-szöget feltételünk szerint felbontva a

B_{1} B_{3}

B_{1} B_{4}

...

B_{1} B_{n - 2}

átló hány felbontásban szerepel?
Előrebocsátjuk, hogy

B

-t minden felbontás

n - 4

átló felhasználásával

n - 3

háromszögre osztja: a háromszögek összesen

3 n - 9

oldalát egyrészt

B

-nek

n - 1

oldala adja, a maradó

2 n - 8 = 2 (n - 4)

oldalt pedig az

n - 4

átló, a két oldalán álló háromszögek mindegyikével számítva. Mármost a

B_{1} B_{k}

átló meghúzása ‐ itt is

3 ≦ k ≦ n - 2

‐ az

(n - 1)

-szöget ugyanúgy egy

k

-szögre és egy

(n - k + 1)

-szögre osztja, mint az

A_{1} A_{2} ... A_{n}

n

-szöget az

A_{1} A_{2} A_{k + 1}

háromszög megrajzolása, tehát a

B_{1} B_{k}

átló

F_{k} \cdot F_{n - k + 1}

felbontásban szerepel. Így az

\begin{matrix} S = F_{3} \cdot F_{n - 2} + F_{4} \cdot F_{n - 3} + ... + F_{k} \cdot F_{n - k + 1} + ... + F_{n - 2} \cdot F_{3} \end{matrix}

számban minden olyan felbontás szerepel, melyben van a

B_{1}

-ből kiinduló átló, mert sorravettük a

B_{1}

-ből kiinduló összes átlókat. Éspedig minden felbontás annyiszor szerepel

S

-ben, ahány ilyen átló van benne. Hasonlóan végigmenve a

B_{2}

B_{3}

...

B_{n - 1}

csúcsokból kiinduló összes átlókon,

(n - 1) S

felbontást számláltunk meg. Ebben a számban már

B

minden felbontása ugyanannyiszor szerepel, éspedig

2 (n - 4)

-szer, mert minden felbontást a benne felhasznált

n - 4

átló mindegyikével számbavettünk, éspedig 2-szer, az átlót az egyik, majd a másik végpontjából meghúzva.

B

felbontásainak száma

F_{n - 1}

, így

\begin{matrix} (n - 1) S = 2 (n - 4) F_{n - 1}, S = \frac{2 (n - 4)}{n - 1} \cdot F_{n - 1}, \end{matrix}

ennélfogva (2)-ből

\begin{matrix} F_{n} = 2 F_{n - 1} + S = \frac{2 (2 n - 5)}{n - 1} \cdot F_{n - 1} . \end{matrix}

Ezt a képletet

n

helyén egymás után

n - 1

-gyel,

n - 2

-vel,

...

utoljára 4-gyel alkalmazva, végül beírva, hogy

F_{3} = 1

, adódik:

\begin{matrix} F_{n} = \frac{2 (2 n - 5)}{n - 1} \cdot \frac{2 (2 n - 7)}{n - 2} \cdot F_{n - 2} = \frac{2^{2} (2 n - 5) (2 n - 7)}{(n - 1) (n - 2)} \cdot \frac{2 (2 n - 9)}{n - 3} \cdot F_{n - 3} = \\ = ... = \frac{2^{n - 3} (2 n - 5) (2 n - 7) (2 n - 9) ... 5 \cdot 3}{(n - 1) (n - 2) ... 4 \cdot 3} . \end{matrix}

Végül bővítéssel, a faktoriális, majd pedig a binomiális együttható jelölésével

F_{n}

így is írható:

\begin{matrix} F_{n} = \frac{2^{n - 2}}{(n - 1)!} \cdot \frac{(2 n - 5) (2 n - 6) (2 n - 7) ... 4 \cdot 3 \cdot 2}{2 (n - 3) \cdot 2 (n - 4) \cdot ... \cdot 2 \cdot 2 \cdot 2 \cdot 1} = \\ = \frac{2 \cdot (2 n - 5)!}{(n - 1)! (n - 3)!} = \frac{1}{n - 2} (\binom{2 n - 4}{n - 3}) . \end{matrix}

Ezeket a végeredményeket néhány versenyző az irodalomban megtalálta és (bizonyítás nélkül) közölte.