Feladat: 1180. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Lehel Csaba ,  Pázmándi László 
Füzet: 1963/szeptember, 10 - 12. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Háromszögek szerkesztése, Feladat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1962/május: 1180. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a keresett háromszög ABC, mérjük rá a BC=a oldal felét az AB=c oldal B-n túli meghosszabbítására és legyen a végpont D. A BCD háromszögben ismerjük a DBC∢=180∘-β szöget és az ezt bezáró oldalak arányát: BD:BC=1:2, így hozzá hasonló háromszöget könnyen szerkeszthetünk, és abból a kiegészített ábrát is megszerkeszthetjük, pl. a következő módon: Egy c+a/2 hosszúságú AD szakasz belsejében levő B1 ponttal, mint csúccsal, mérjük fel β-t úgy, hogy egyik szára B1A legyen, és mérjük fel a másik szárra a B1C1=2B1D szakaszt (1. ábra). A C pontot a DC1=f félegyenesből az A körüli b sugarú k körrel metszhetjük ki, B-t pedig az AD szakaszból a C-n át C1B1-gyel párhuzamosan húzott egyenessel. Nyilvánvaló, hogy a kapott háromszög megfelel a feltételeknek.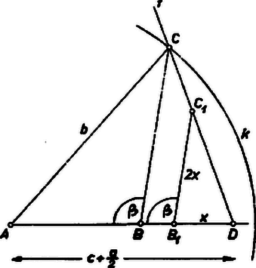

 
 
1. ábra
 

f és k (D-től különböző) metszéspontjainak száma 0, 1, 2, aszerint, hogy k nem metszi f-ot, ill. éppen érinti, ill. 2 pontban metszi, végül ismét 1 akkor, ha b≧c+a/2, mert így a második metszés C1D-nek D-n túli meghosszabbítására esnék. Amennyiben az ADC1 szög tompaszögnek adódik, akkor nem lehet 1-nél több megoldás. Másrészt a megoldások számát az is csökkentheti, ha az f-en kiadódott, D-től különböző C-n át a mondott párhuzamost meghúzva, ez DA-t A-ban, vagy az A-n túli meghosszabbításon metszi.
 
 Pázmándi László (Budapest, József A. g.)
 

Megjegyzés: Könnyű belátni, hogy β=120∘ mellett ADC1∢<90∘, és nyilván β>120∘ mellett lesz 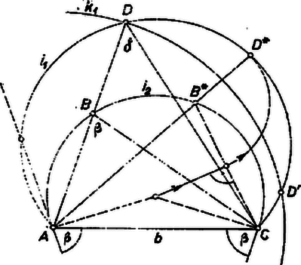ADC1∢>90∘.
 
 
2. ábra
 

II. megoldás. Az előző megoldásban szereplő kiegészített ábrát a következő módon is megszerkeszthetjük. Szerkesztünk egy háromszöget, amelynek egyik szöge 180∘-β, és az ezt bezáró két oldal egyike a másik kétszerese (az előző megoldás B1C1D háromszöge, 2. ábra). A kétszeres oldallal szemközti δ szög akkora, amekkora alatt az AC=b hosszúságú oldal D-ből látszik. Ezért az ACD háromszöget megszerkeszthetjük úgy, hogy egy b hosszúságú AC szakasz fölé egyik oldalán δ látószögű i1 körívet szerkesztünk. Ebből az A körül c+a/2 sugárral rajzolt k1 kör metszi ki D-t (l, 2, vagy 0 metszéspont lehet). B-t AD-ből pl. az AC fölött β látószögű i2 körívvel metszhetjük ki.
A szerkesztés egy célszerű végrehajtása: az AC=b szakaszhoz β nyílású i2 látószög körívet szerkesztünk (elég az egyik oldalán), legyen ennek tetszés szerinti (belső) pontja B*. AB*-nak B*-on túli meghosszabbítására rámérjük a B*C szakasz felével egyenlő B*D* szakaszt, ekkor i1 az ACD* háromszög körülírt körének a D*-ot tartalmazó AC íve. A fenti k1 kör i1-ből kimetszi D-t, és a DA szakasz i2 -ből B-t. (Így az i2 körívet kétszer használtuk fel.)
i2 mindig az i1-gyel és az AC húrral határolt körszeletben van, mert β=δ+BCD∢>δ. ‐ Legfeljebb annyi megoldás van, amennyi az i1 és k1 közös pontjainak száma (C természetesen nem fogadható el D gyanánt). Előfordulhat, hogy D előáll, de nem tartozik hozzá B, ti. akkor, ha D az i2-höz A-ban húzott érintőnek i2-t nem tartalmazó partján adódik, vagy ezen az érintőit magán. Ha a fenti δ tompaszög, akkor i1 kisebb félkörnél, így bármely az egyik végpontja körül irt kör legfeljebb egy pontban metszi.
 
 Lehel Csaba (Budapest, Apáczai Csere J. gyak. g.)
 

Megjegyzés. Több versenyző bonyolult számítások alapján végezte el a szerkesztést. A fenti megoldásokhoz a megoldhatóságnak, ill. a megoldások különböző számának feltételeit geometriai módon adtuk meg, az adatokból felírható egyenlőtlenségek közlését mellőztük.