Feladat: 1179. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Aleva Gy. ,  Aleva György ,  Ámon Magdolna ,  Benczúr András ,  Berecz Ágota ,  Bodoky Andrea ,  Dobó Ferenc ,  Fazekas P. ,  Fejéregyházi Sándor ,  Fodor J. ,  Fodor János ,  Gálfi László ,  Gerencsér László ,  Gyárfás András ,  Lehel Cs. ,  Lehel Jenő ,  Major J. ,  Makai Endre ,  Malatinszky Gábor ,  Máté Attila ,  Nagy Dénes L. ,  Négyessy M. ,  Nováky Béla ,  Papp L. ,  Sebestyén Zoltán ,  Seprődi László ,  Szepesvári István ,  Szidarovszky Ágnes ,  Tamás Géza ,  Zalán Péter 
Füzet: 1963/október, 51 - 53. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Tengelyes tükrözés, Diszkusszió, Háromszögek szerkesztése, Feladat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1962/május: 1179. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az adott szög MON∢=ω<90∘, a feltételnek megfelelő ABC egyenlő szárú háromszög BC alapja legyen az OM száron, B közelebb O-hoz, az A csúcs az ON száron; az AB száron fekvő adott pont legyen 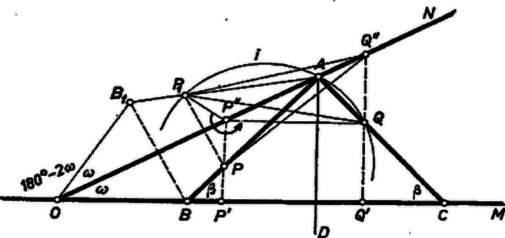P, az AC-n fekvő Q.

 
 
1. ábra
 

A háromszög egyenlő szárú voltából következik, hogy β=ABC∢=ACB∢ és OBA∢=180∘-β. Ábránkat úgy alakíthatjuk át, hogy az utóbbi két szög, melyek összege 180∘, egy négyszög két szögébe menjen át, s így a másik két szög között is összefüggést állapíthatunk meg. Tükrözzük B-t AO-ra, legyen a tükörképe B1. Ekkor az AB1OC négyszög C-nél, O-nál, ill. B1-nél levő szöge β, 2ω, ill. 180∘-β s így az A-nál levő szög 180∘-2ω, ami az adatokból megszerkeszthető. Ennek a szögnek AC szára átmegy Q-n, az AB1 szár pedig átmegy P-nek az OA-ra vonatkozó P1 tükörképén.
Ezek szerint A-t ON-ből a P1Q szakasz fölé írt 180∘-2ω nyílású i látószögkörív metszi ki, B-t és C-t pedig AP, ill. AQ metszi ki OM-ből.
Az ABC háromszög megfelel a követelményeknek, mert a PAQ szög felezőjének egy pontját D-vel jelölve
DAO∢=PAO∢+QAP∢2=PAO∢+(PAO∢+QAP∢)2==P1AO∢+QAO∢2=P1AQ∢2=90∘-ω,


tehát AD⊥OM, vagyis AD⊥BC, az ABC háromszög egyenlő szárú.
ω hegyes szög, ezért a P1AQ szög 0∘ és 180∘ közé esik. Így az i ív a P1Q egyenesnek O-val ellentétes partján szerkesztendő, ugyanis O benne van a 180∘-nál kisebb P1AQ szög terében. i mindig metszi az ON félegyenest, mert végpontjait ON szétválasztja, ugyanezért mindig pontosan egy metszéspontot kapunk A céljára.
A mindig a P és Q-n át OM-re állított merőlegesnek ON-nel való P'', Q'' metszéspontjai között adódik, tehát mindig megfelelő háromszöget kapunk. Ugyanis P1Q-nak Q''-ből vett látószöge kisebb a P1AQ szögnél, P''-ből vett látószöge pedig nagyobb nála. (Az utóbbi esetben azt a szögtartományt értjük a látószögön, amelynek O belső pontja.) Valóban

P1Q''Q∢=P1Q''O∢+OQ''Q∢=PQ''O∢+QQ''O∢<2QQ''O∢==2(90∘-ω)=P1AQ∢,


mert feltevésünk szerint P benne van az OQ'Q'' háromszögben. Másrészt ugyanezért
P1P''Q∢=P1P''P∢+PP''Q∢>P1P''P∢=2OP''P∢=P1AQ∢.

Ha P'' egybeesik Q''-vel, vagyis PQ⊥OM, akkor egyenlőtlenségeink helyén egyenlőség áll, A azonos P''-vel, a megoldás egyenesszakasszá fajul.
Még egy megoldást kapunk, ha egyenlő szárú háromszögünk alapját az ON száron keressük. Az imént mondott elfajulás csak az egyik esetben következhet be.
 
 Benczúr András (Budapest, Fazekas M. g.)
 dolgozatából, a diszkussziót kiegészítve
 

Sok számolásos megoldás érkezett. Egy ilyet vázolunk, a diszkussziót az olvasóra bízzuk.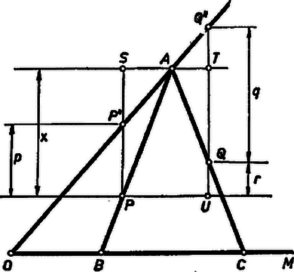
 
 
2. ábra
 
II. megoldás. Húzzunk párhuzamost OM-mel A-n és P-n át, legyen P és Q vetülete az előbbin S, ill. T, Q vetülete az utóbbin U. Az APS, AQT és az AP''S, AQ''T háromszögpárok nyilvánvaló hasonlóságából:
PSQT=ASAT=P''SQ''T,
ezért PS=x, P''P=p, Q''Q=q, QU=r jelöléssel (r negatív is lehet):
xx-r=x-pq+r-x,2x2-(p+q+2r)x+pr=0,x=14(p+q+2r±(p+q+2r)2-8pr).


 Sebestyén Zoltán (Celldömölk, Berzsenyi D. g.)