Kezdőlap


Feladat:	1174. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Benczúr András , Demendy Z. , Fejéregyházi Sándor , Gálfi László , Gyárfás András , Lehel J. , Nováky Béla , Pázmándi László , Sebestyén Zoltán , Szidarovszky Ágnes , Szidarovszky Ferenc , Zalay Miklós
Füzet:	1963/március, 117 - 120. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Húrsokszögek, Érintősokszögek, Koszinusztétel alkalmazása, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1962/április: 1174. matematika feladat

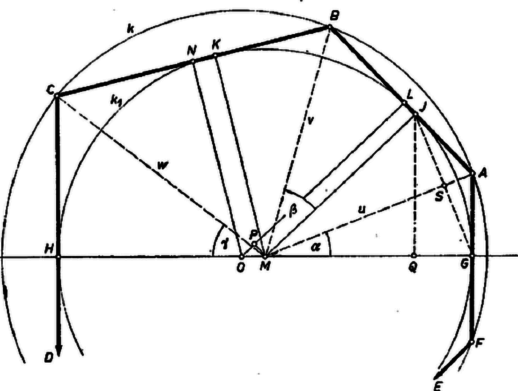
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel, hogy az $A B C D E F$ hatszögre teljesülnek a feladat feltételei, $k$ körülírt körének középpontja $O$ , $k_{1}$ beírt körének középpontja $M$ és szimmetriatengelye az $A F$ és $C D$ oldalak $G$ , ill. $H$ felezőpontját összekötő egyenes. $G H$ -n tükrözve a hatszög önmagába megy át, ezért $k$ és $k_{1}$ is, ennélfogva $O$ és $M$ a $G H$ -n vannak. Legyen továbbá $M$ vetülete $A B$ -re $J$ , $B C$ -re $K$ (ezek $k_{1}$ érintési pontjai), továbbá $O$ vetülete ugyanezen oldalakra (az oldalak felezőpontja) $L$ , ill. $N$ . Ha a betűzést úgy választjuk, hogy $M$ az $O G$ szakaszon legyen, vagy éppen $O$ -ban, akkor pontjaink sorrendje a hatszög kerületén a következő: $A$ , $J$ , $L$ , $B$ , $K$ , $N$ , $C$ . Így

\begin{matrix} \begin{matrix} A L = L B -ből & és & B N = N C -ből : \\ A J + J L = B J - J L & és & B K + K N = C K - K N, \\ B J = A J + 2 J L, & B K = C K - 2 K N, \end{matrix} \end{matrix}

végül, mivel

B J = B K

, továbbá

A J = A G

és

C K = C H

, azért

\begin{matrix} A G + 2 J L = A J + 2 J L = B J = B K = C K - 2 K N = C H - 2 K N, \end{matrix}

azaz

\begin{matrix} A G + 2 J L = C H - 2 K N . \end{matrix}

(2)

Az itt fellépő szakaszokat az alábbiakban kifejezzük

R

r

és

c

-vel, így (2)-ből összefüggést kapunk ezen három hosszúság között. Az

O A G

és

O C H

derékszögű háromszögekből

\begin{matrix} A G = \sqrt[]{R^{2} - {(r + c)}^{2}}, C H = \sqrt[]{R^{2} - {(r - c)}^{2}} . \end{matrix}

(3)

Jelöljük

M

-nek

O L

-en való vetületét

P

-vel,

J

-nek

H G

-n levő vetületét

Q

-val és az

M G A J

deltoid átlóinak metszéspontját

S

-sel. Így

J L = M P

, továbbá

M P O

és

J Q M

háromszögek hasonlók, ezért

\begin{matrix} \frac{J L}{O M} = \frac{M P}{O M} = \frac{J Q}{M J} = \frac{J Q}{M G}, J L = \frac{O M \cdot J Q}{M G} = \frac{c \cdot J Q}{r} . \end{matrix}

J Q

-t más szakaszokkal fejezhetjük ki az

M G J

háromszög kétszeres területének kétféleképpen való felírása alapján :

\begin{matrix} J Q = \frac{G J \cdot M S}{M G}; \end{matrix}

hasonlóan az itt fellépő

G J

-t az

M G A J

deltoid területének kétféleképpen való felírásával, figyelembe véve, hogy a szimmetriatengely az idomot két derékszögű háromszögre bontja fel:

\begin{matrix} \frac{1}{2} \cdot G J \cdot A M = M G \cdot A G = r \cdot A G, G J = \frac{2 r \cdot A G}{A M}; \end{matrix}

végül

M S

-t az

A M G

derékszögű háromszögből:

\begin{matrix} M S = \frac{M G^{2}}{A M} = \frac{r^{2}}{A M} . \end{matrix}

Ezekkel

\begin{matrix} J L = \frac{c}{r} \cdot \frac{G J \cdot M S}{r} = \frac{2 c r \cdot A G}{A M^{2}} = \frac{2 c r \cdot A G}{r^{2} + A G^{2}}, \end{matrix}

végül (3) alapján

\begin{matrix} J L = \frac{2 c r \sqrt[]{R^{2} - {(r + c)}^{2}}}{R^{2} - 2 c r - c^{2}} . \end{matrix}

(4)

Ugyanígy kapjuk

K N

kifejezését:

\begin{matrix} K N = \frac{2 c r \cdot C H}{C M^{2}} = \frac{2 c r \sqrt[]{R^{2} - {(r - c)}^{2}}}{R^{2} + 2 c r - c^{2}} . \end{matrix}

(5)

A (2)‐(5) eredmények alapján

R, r

és

c

között a következő összefüggés áll fenn:

\begin{matrix} (1 + \frac{4 c r}{R^{2} - 2 c r - c^{2}}) \cdot \sqrt[]{R^{2} - {(r + c)}^{2}} = (1 - \frac{4 c r}{R^{2} + 2 c r - c^{2}}) \cdot \sqrt[]{R^{2} - {(r - c)}^{2}} . \end{matrix}

Innen összevonással, a törtek eltávolításával és

(R^{2} - c^{2})

hatványai szerinti rendezéssel:

\begin{matrix} {(R^{2} - c^{2} + 2 c r)}^{2} \sqrt[]{R^{2} - {(r + c)}^{2}} = {(R^{2} - c^{2} - 2 c r)}^{2} \sqrt[]{R^{2} - {(r - c)}^{2}}, \end{matrix}

\begin{matrix} [{(R^{2} - c^{2})}^{2} + 4 c r (R^{2} - c^{2}) + 4 c^{2} r^{2}] \sqrt[]{(R^{2} - c^{2}) - (r^{2} + 2 c r)} = \end{matrix}

\begin{matrix} = [{(R^{2} - c^{2})}^{2} - 4 c r (R^{2} - c^{2}) + 4 c^{2} r^{2}] \sqrt[]{(R^{2} - c^{2}) - (r^{2} - 2 c r)} . \end{matrix}

Végül négyzetreemeléssel és rendezéssel a bizonyítandó összefüggést kapjuk.

Benczúr András (Budapest, Fazekas M. gyak. g. IV. o. t.)

II. megoldás. Vezessük be a következő jelöléseket:

G M A ∢ = A M J ∢ = α

J M B ∢ = B M K ∢ = β

K M C ∢ = C M H ∢ = γ

M A = u

B M = v

M C = w

. Így

cos α = r / u

cos β = r / v

cos γ = r / w

, és az

O M A

O M C

háromszögekből a koszinusz tétellel

O A^{2} = R^{2} = c^{2} + u^{2} + 2 c r

O C^{2} = R^{2} = c^{2} + w^{2} - 2 c r

, tehát

\begin{matrix} u^{2} = R^{2} - c^{2} - 2 c r, w^{2} = R^{2} - c^{2} + 2 c r . \end{matrix}

(6)

Hasonlóan az

O M B

háromszögből

\begin{matrix} O B^{2} = R^{2} = c^{2} + v^{2} + 2 c v cos (2 α + β) . \end{matrix}

Innen, tekintettel arra, hogy

α + β + γ = 90^{\circ}

, amiből

2 α + β = 90^{\circ} - (γ - α)

, továbbá

v = r / cos β = r / sin (α + γ)

-val

\begin{matrix} (R^{2} - c^{2}) sin^{2} (α + γ) - r^{2} = 2 c r sin (γ - α) \cdot sin (α + γ) = \end{matrix}

(7)

\begin{matrix} = c r (cos 2 α - cos 2 γ) = c r (2 cos^{2} α - 2 cos^{2} γ) = 2 c r (\frac{r^{2}}{u^{2}} - \frac{r^{2}}{w^{2}}) = \end{matrix}

\begin{matrix} = \frac{2 c r^{3} (w^{2} - u^{2})}{u^{2} w^{2}} = \frac{8 c^{2} r^{4}}{u^{2} w^{2}} . \end{matrix}

A bal oldal átalakítására felhasználjuk, hogy

\begin{matrix} sin α = \frac{1}{u} \sqrt[]{u^{2} - r^{2}}, sin γ = \frac{1}{w} \sqrt[]{w^{2} - r^{2}}, \end{matrix}

\begin{matrix} sin (α + γ) = \frac{r}{u w} (\sqrt[]{u^{2} - r^{2}} + \sqrt[]{w^{2} - r^{2}}) . \end{matrix}

ennélfogva (6) alapján a következő összefüggést kapjuk:

\begin{matrix} (R^{2} - c^{2}) {(\sqrt[]{R^{2} - c^{2} - 2 c r - r^{2}} + \sqrt[]{R^{2} - c^{2} + 2 c r - r^{2}})}^{2} = \end{matrix}

\begin{matrix} = 8 c^{2} r^{2} + u^{2} w^{2} = {(R^{2} - c^{2})}^{2} + 4 c^{2} r^{2} . \end{matrix}

Innen a szokásos rendezési lépésekkel ismét (1) adódik.

Zalay Miklós (Budapest, Hengersor úti g. IV. o. t.)

Megjegyzés. Bizonyítás nélkül közöljük, hogy (1) minden olyan hatszögre érvényes, amelybe, és köréje is, kör írható. Ezen túlmenően érvényes a következő: ha

R

r

és

c

teljesítik (1)-et, az egymástól

c

távolságra levő

O_{1}

és

O_{2}

pontok körül

R

, ill.

r

sugárral írt kör

k_{1}

, ill.

k_{2}

, és

A B C D E F

olyan a

k_{1}

-be írt konvex hatszög, melynek

A B

B C

C D

D E

és

E F

oldalai érintik

k_{2}

-t, akkor

F A

oldala is érinti

k_{2}

-t.