Feladat: 1165. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Chikán Attila 
Füzet: 1962/november, 131 - 132. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Szabályos sokszögek szerkesztése, Feladat
Hivatkozás(ok):Feladatok: 1962/március: 1165. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott ABCD=R rombusznak legalább az egyik oldalára az EFGHK=P szabályos ötszögnek legalább két csúcsa esik, és világos, hogy egy oldalára legfeljebb két, mégpedig két szomszédos ötszögcsúcs esik. Válasszuk a betűzést úgy, hogy a rombusz AB oldalán legyen az ötszög EF oldala, és A-nál 72∘-os szög legyen. Így G nem lehet a CD oldalon, mert akkor H a rombuszon kívül lenne, tehát BC-n kell lennie.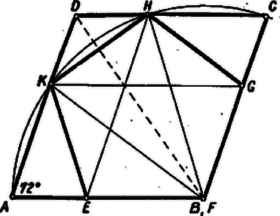

 
 

Mivel ABC∢=108∘=EFG∢, ez csak úgy lehet, ha F a B csúcsba esik. Az ötszögből a rombuszt tehát úgy kapjuk, hogy az ötszög EF és FG oldalát meghosszabbítjuk és ezeket elmetsszük a H-n át EF-fel és a K-n át FG-vel húzott párhuzamossal. Be kell látnunk, hogy az így keletkező paralelogramma valóban rombusz. Ez következik abból, hogy az ábrát az ötszög F-ből induló szögfelezőjére tükrözve egyfelől EF és FG, másfelől H és K egymás tükörképei lesznek, párhuzamos egyeneseknek pedig a képei is párhuzamosak, tehát a paralelogramma önmagába megy át, így az EF és FG egyenesen levő oldalai egyenlők, tehát a négyszög rombusz (és a tükrözési tengely átlója).
Ha R van adva, akkor P-t könnyen megszerkeszthetjük, ha megfigyeljük még, hogy BCH és (ABK) egyenlő szárú háromszög. Ugyanis BH∥EK, s így BHC∢=KEA∢=180∘-108∘=72∘=BCH∢, tehát BC=BH(=BK). Így H-t és K-t a B körül BC sugárral írt körrel metszhetjük ki a CD és DA oldalból, majd E-t, ill. G-t a H-n át BC-vel, ill. K-n át AB-vel párhuzamosan húzott egyenessel AB-ből, ill. BC-ből.
Jelöljük a rombusz oldalát c-vel, az ötszögét a-val. Az éppen felhasznált BCH háromszögből GH hozzá hasonló HCG háromszöget metsz le,1 mert HGC∢=72∘=HCG∢, így HC=HG=a, és
HCBC=GCHC,HC2=BC⋅GC,azaza2=c(c-a).
Ezt a szerint rendezzük és a-ra megoldjuk (a pozitív gyököt véve):
a2+ac-c2=0,a=5-12c.

 Chikán Attila (Eger, Gárdonyi G. g. IV. o. t.)
 
Megjegyzés. Figyeljük meg, hogy az adott paralelogrammáról nem lett volna szükséges kikötni, hogy rombusz, ez következett a szögek ismeretében abból, hogy szabályos ötszöget lehet beleírni.
1Ugyanezt a számítást végeztük el az 1157. feladatban cos 36∘ kiszámításához. Lásd ezen számunk 118. oldalát.