Kezdőlap


Feladat:	1160. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kármán Antal
Füzet:	1962/november, 124 - 125. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1962/január: 1160. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 3 kiemelt résztest és a maradéktest térfogatai egyenlők, tehát mindegyiké $1 / 4 {dm}^{3}$ . Az először kiemelt résztest tömör négyzetes oszlop, térfogata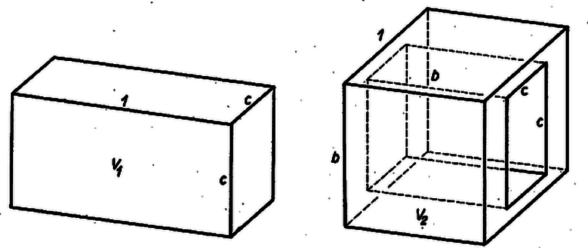

\begin{matrix} V_{1} = c^{2} \cdot 1 = 1 / 4, innen c = 1 / 2. \end{matrix}

Másodszor

b

alapélű, 1 magasságú négyzetes oszlopot kell kivágni, amibe azonban beleesik az előbb kifaragott négyzetes oszlop egy része is. Így, ha ismét

1 / 4 {dm}^{3}

anyagot akarunk kivágni, akkor minden esetre

b > 1 / 4 = c

élű négyzetes oszlopot kell belefaragnunk a kockába. Az ebbe eső, már üres rész egy

c

alapélű,

b

magasságú négyzetes oszlop. Az eltávolított anyag térfogata tehát ‐ ami ismét a kocka negyede kell, hogy legyen ‐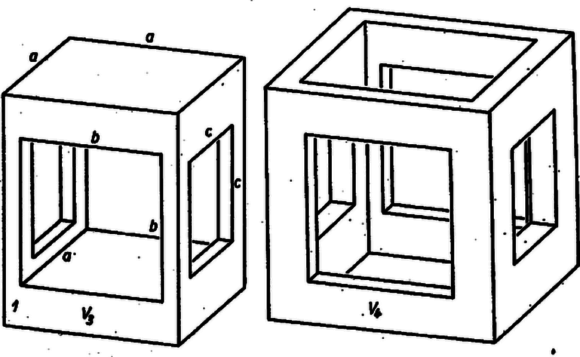

\begin{matrix} V_{2} = b^{2} - c^{2} b = b^{2} - \frac{b}{4} = \frac{1}{4}, \end{matrix}

ennek pozitív gyöke

\begin{matrix} b = \frac{1 + \sqrt[]{17}}{8} \approx 0, 640. \end{matrix}

Hasonlóan nyilvánvaló, hogy

a > b

. A harmadszor kiemelt résztesten már két négyzetes oszlop alakú átfúrás van, tengelyeik egymásra merőlegesek. Külön‐külön

c^{2} a

, ill.

b^{2} a

az űrtartalmuk, ha azonban

V_{3}

-at ezeknek

a_{2}

-ből való levonásával számítanak, a második résztesten levő lyuk térfogatát 2-szer vonnánk le, ezért 1-szer vissza kell adnunk:

\begin{matrix} V_{3} = a^{2} - c^{2} a - b^{2} a + c^{2} b = \frac{1}{4} . \end{matrix}

c

és

b

talált értékeinek behelyettesítésével

\begin{matrix} 32 a^{2} - (17 + \sqrt[]{17}) a - (7 - \sqrt[]{17}) = 0, \end{matrix}

(1)

és a pozitív gyök:

\begin{matrix} a = \frac{17 + \sqrt[]{17} + \sqrt[]{1202 - 94 \sqrt[]{17}}}{64} \approx 0, 776. \end{matrix}

Kármán Antal (Jászberény, Lehel Vezér g. IV. o. t.)

Megjegyzések. 1. Ábráink az (egy darabban kiemelve gondolt) résztesteket ábrázolják, tekinthetők azonban az eredeti testben létrejött üregek képének is. Ebben az értelemben a 3. résztest ,,középső'' részére is ráillik a kissé tréfásan emlegetett ,,lyukban levő lyukban levő lyuk'' kifejezés.
2. Az (1) egyenletet a maradéktest térfogatából is megkaphatjuk. Ez a kockából az

a^{2}

térfogatú négyzetes oszlop és 4 ,,ablaktér'' térfogatának elvételével marad vissza. Az ablakok területe

c^{2}

, ill.

b^{2}

, ,,mélységük'' pedig

(1 - a) / 2

. Így

\begin{matrix} V_{4} = 1 - a^{2} - (c^{2} + b^{2}) (1 - a) = 1 / 4. \end{matrix}