Kezdőlap


Feladat:	1159. matematika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Jankó Mihály
Füzet:	1962/november, 122 - 124. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Mértani helyek, Feladat
Hivatkozás(ok):	Feladatok: 1962/január: 1159. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $e$ és $g$ egyenestől mért távolságok kisebbikén, ha a két távolság egyenlő, ezek közös értékét fogjuk érteni a szokásnak megfelelően. Jelöljük az adott távolságot $d$ -vel, a téglalap $e$ -vel, ill. $f$ -fel párhuzamos szimmetriatengelyét $e_{1}$ -gyel, ill. $f_{1}$ -gyel (1. ábra). Vizsgáljuk először azokat a $P$ pontokat, amelyek nincsenek messzebb $e$ -től, mint $g$ -től, sem $f$ -től nincsenek messzebb, mint $h$ -tól. Ezek $e_{1}$ -nek azon az oldalán vannak, amelyiken $e$ , másrészt $f_{1}$ nek azon az oldalán, mint $f$ (hozzávéve az $e_{1}$ és $f_{1}$ egyenes megfelelő részeit is), vagyis az $e_{1}$ és $f_{1}$ meghatározta abban a $T_{1}$ síknegyedben, a határokat is hozzávéve, amelybe $e$ és $f$ metszéspontja esik. A keresett mértani hely ide eső részéből a többi rész a szimmetriaviszonyok alapján már könnyen fog adódni.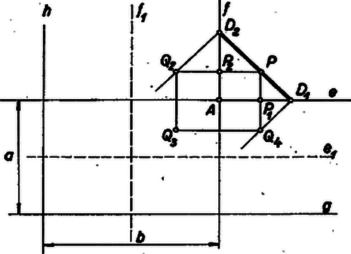

1. ábra

Két pontnak, amelyek egymás tükörképei

e

-re vagy

f

-re, vagy a két egyenes

A

metszéspontjára, egyenlő a távolsága

e

-től is,

f

-től is, így vagy mindegyik hozzátartozik a mértani helyhez, vagy egyik sem. Elég tehát az

e

és

f

közti egyik síknegyedet vizsgálni. Vegyük azt, amelyiken sem

e_{1}

, sem

f_{1}

nem megy át (ez teljesen benne van

T_{1}

ben).
Az

e

-n és

f

-en

A

-tól

d

távolságra levő

D_{1}

és

D_{2}

pont nyilván a mértani helyhez tartozik. Legyen

P

a mértani hely egy további pontja a vizsgált síkrészben, és

P

vetülete

e

-n, ill.

f

-en

P_{1}

, ill.

P_{2}

. Mivel

A P_{1} P P_{2}

téglalap, azért

d = P P_{1} + P P_{2} = P P_{1} + A P_{1}

. Másrészt

d = A D_{1} = A P_{1} + P_{1} D_{1}

, tehát

P P_{1} = P_{1} D_{1}

, s így

P P_{1} D_{1}

egy egyenlő szárú derékszögű háromszög, tehát

P D_{1} P_{1} ∢ = 45^{\circ}

. Ez azt jelenti, hogy a mértani hely

P

pontjai a

D_{1} D_{2}

egyenesszakaszon vannak.
Legyen a szakasz egy tetszés szerinti pontja

P^{*}

, vetülete

e

-n,

f

-en

P_{1}^{*}

P_{2}^{*}

, akkor

P^{*} P_{1}^{*} D_{1}

egyenlő szárú derékszögű háromszög, s így

P^{*} P_{1}^{*} + P^{*} P_{2}^{*} = P_{1}^{*} D_{1} + A P_{1}^{*} = A D_{1} = d

, tehát

P^{*}

a mértani helyhez tartozik. A mértani helynek a vizsgált síkrészbe eső része tehát a

D_{1} D_{2}

egyenesszakasz. A

T_{1}

be eső további része e szakasz

e

-re,

f

-re és az

A

pontra vonatkozó tükörképéből annyi, amennyi még

T_{1}

-hez tartozik. Ez egy négyzet kerülete, melynek átlói az

e

és az

f

egyenesen vannak és

2 d

hosszúságúak, feltéve, hogy

d

nem nagyobb az

e

és

g

egyenesek

a

távolságának, sem az

f

és

h

egyenesek

b

távolságának felénél, különben e négyzet kerületének a

T_{1}

-be eső (esetleg nem is összefüggő) részeiből áll.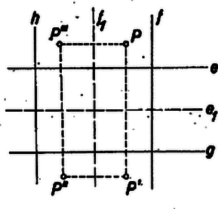

2. ábra

Legyen most már

P

T_{1}

egy tetszés szerinti pontja és

P'

e_{1}

re vonatkozó tükörképe (2. ábra). Ekkor

P

és

P'

távolsága

f

-től és

h

-tól megegyezik, továbbá egyenlő

P

-nek

e

-től és

P'

-nek

g

-től mért távolsága, és hasonlóan

P

-nek

g

-től és

P'

-nek

e

-től való távolsága. Így

P

és

P'

vagy mindkettő a mértani helyhez tartozik, vagy egyik sem. Hasonló érvényes

P'

-nek

f_{1}

re vett

P''

tükörképére és

P''

-nek

e_{1}

-re vett

P''

tükörképére is. A teljes mértani helyet ezek szerint úgy kapjuk, hogy a mértani hely

T_{1}

be eső részét

e_{1}

-re tükrözzük, majd a tükörképet

f_{1}

-re tükrözzük és a második tükörképet újra

e_{1}

-re. Aszerint, hogy

a

b

d

és

a + b

között rendre

2 d ≦ b ≦ a

, ill. a

b < 2 d < a

, ill.

b < a < 2 d < a + b

, ill.

2 d > a + b

nagyságviszony áll fenn, a mértani hely a 3‐6. ábrák szerint alakul,

2 d = a + b

esetén a mértani helynek az adott téglalap középpontjában elszigetelt pontja van.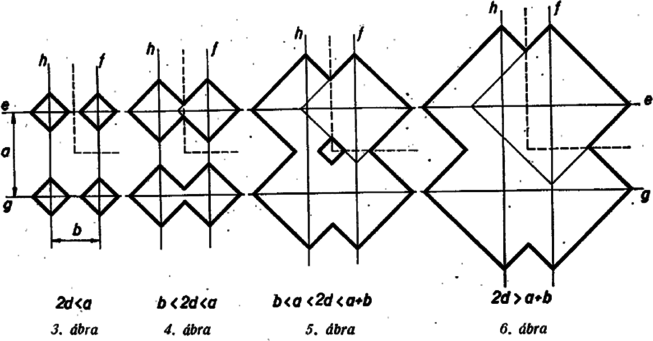

Jankó Mihály (Szentendre, Móricz Zs. g. III. o. t.)