Kezdőlap


Feladat:	1158. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bán Tamás , Benczúr András , Berecz Ágota , Bodoky Andrea , Böröczky György , Demendy Zoltán , Egerszegi Piroska , Fazekas P. , Fodor J. , Gálfi László , Gerencsér L. , Horváth Péter , Huber Tibor , Jójárt István , Kunszt Zoltán , Kuzmann E. , Lehel J. , Malatinszky G. , Nárai György , Nováky Béla , Pázmándi L. , Raisz M. , Reuss P. , Rozváczy Judit , Sebestyén Zoltán , Surányi Andor , Szekeres Veronika , Szidarovszky Ágnes , Szidarovszky Ferenc , Tamás Géza , Varga L. , Vincze I. , Zalán F. Á. , Zalán Péter
Füzet:	1962/november, 120 - 122. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Szögfelező egyenes, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1962/január: 1158. matematika feladat

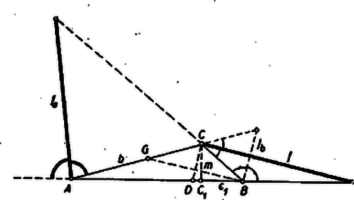
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Célszerű a külső szögfelező szóban forgó szakaszát az oldalakkal általában kifejezni, mert bár számpéldáról van szó, de a számítást háromszor kell elvégeznünk. Messe az $A B C$ háromszögben a $C$ -ből húzott belső, ill. külső szögfelező az $A B$ egyenest $D$ , ill. $E$ -ben,^{$^{*}$} legyen $C E = f$ , továbbá a $C$ -ből húzott magasság $C C_{1} = m$ . A szokásos jelöléseket használva feltehetjük, hogy $a < b$ (egyenlőség esetén $E$ nem léteznék), így $a < β$ , ezért $C D B ∢ = γ / 2 + α < γ / 2 + β = C D A ∢$ , tehát $C D B$ hegyesszög, $D$ az $A C_{1}$ szakaszon van, $E$ pedig $A B$ -nek $B$ -n túli meghosszabbításán, mert $C E ⊥ C D$ . $f$ -et a $C E C_{1}$ derékszögű háromszögből számítjuk, evégett a $C C_{1}$ és $C_{1} E$ befogókat kifejezzük az oldalakkal. Legyen a $B E$ szakasz hossza $e$ , és $B C_{1} = c_{1}$ (az utóbbit előjellel értve, éspedig a $B A$ irányt véve pozitívnak), így a $C C_{1} A$ és $C C_{1} B$ derékszögű háromszögekből

\begin{matrix} m^{2} = b^{2} - {(c - c_{1})}^{2} = a^{2} - c_{1}^{2}, és innen \\ c_{1} = \frac{a^{2} + c^{2} - b^{2}}{2 c} . & (1) \end{matrix}

Mérjük fel másrészt

C B

-t

C A

-ra és legyen a végpont

G

. Ekkor a

B C G △

egyenlő szárú,

G B ⊥ C D ⊥ C E

, ezért

G B ∥ C E

, és az

A B G

A E C

háromszögek hasonlók.

Így

\begin{matrix} A B : A G = A E : A C, c : (b - a) = (c + e) : b, és & (2) \\ e = \frac{a c}{b - a} . & (3) \end{matrix}

Most már a

C E C_{1} △

-ből, majd (1) és (3) felhasználásával és a szokásos

a + b + c = 2 s

jelöléssel

\begin{matrix} f^{2} = m^{2} + {(e + c_{1})}^{2} = (m^{2} + c_{1}^{2}) + 2 e c_{1} + e^{2} = a^{2} + 2 e c_{1} + e^{2} = \\ = & a^{2} + \frac{(a^{2} + c^{2} - b^{2}) a}{b - a} + \frac{a^{2} c^{2}}{{(b - a)}^{2}} = \frac{a b}{{(b - a)}^{2}} (c^{2} - a^{2} + 2 a b - b^{2}) = \\ = & \frac{a b [c^{2} - {(a - b)}^{2}]}{{(b - a)}^{2}} = \frac{a b (c - a + b) (c + a - b)}{{(b - a)}^{2}} = \\ = & \frac{4 a b (s - a) (s - b)}{{(b - a)}^{2}} . & (4) \end{matrix}

Könnyű belátni, hogy eredményünk

a > b

esetén is érvényes. Ekkor ugyanis

E

A B

-nek

A

-n túli meghosszabbításán van, ezt fejezi ki, hogy (3)-ból

e

-t negatívnak kapjuk.^{$^{*}$} Ez azonban (4)-ben már nem okoz változást. Az

a < b

feltevést máshol nem használtuk fel. Eszerint (4) minden

a \neq b

esetre érvényes. Így az

A

csúcsból húzott

f_{a}

és a

B

-ből húzott

f_{b}

külső szögfelezőszakasz hosszának négyzete (4)-ből a betűk ciklikus felcserélésével

\begin{matrix} f_{a}^{2} = \frac{4 b c (s - b) (s - c)}{{(c - b)}^{2}}, f_{b}^{2} = \frac{4 c a (s - c) (s - a)}{{(a - c)}^{2}}, \end{matrix}

hacsak

c \neq b

, ill.

a \neq c

.
Ha már most

a = 5 - \sqrt[]{7}

b = 6

c = 5 + \sqrt[]{7}

, akkor

f_{a} = 4 \sqrt[]{3} (\approx 6, 928)

f_{b} = 6 / \sqrt[]{7} (\approx 2, 268)

f_{c} = f = 4 \sqrt[]{3} (\approx 6, 928)

. Eszerint a legnagyobb és a legkisebb szög csúcsából húzott külső szögfelezőszakasz egyenlő.

Zalán Péter (Aszód, Petőfi S. g. IV. o. t.) dolgozatából
egyszerűsítéssel és kiegészítéssel.

Megjegyzés. Lényegében ugyanígy jártak el azok, akik

C E

-t a

C E B △

-ből a koszinusz‐tétellel számították és ehhez cos

C B E ∢

-et az

A B C △

-ből fejezték ki.

II. megoldás. A fenti (4) eredményhez szögek ismeretét feltételezve trigonometriai összefüggések alapján is eljuthatunk, ha az így nyert kifejezésekben a szögfüggvényeket ismét az oldalakkal fejezzük ki. Az

A B C

és

B E C

háromszögek együttes területe egyenlő az

A E C △

területével. Mindegyiket 2-szer véve

\begin{matrix} a b sin γ + a f sin B C E ∢ = b f sin A C E ∢ . \end{matrix}

Itt

B C E ∢ = D C E ∢ - D C B ∢ = 90^{\circ} - γ / 2

, és

A C E ∢ = 90^{\circ} + γ / 2

, ezért

\begin{matrix} 2 a b sin \frac{γ}{2} cos \frac{γ}{2} + a f cos \frac{γ}{2} = b f cos \frac{γ}{2}, \end{matrix}

és mivel

γ / 2 < 90^{\circ}

cos γ / 2 \neq 0

, egyszerűsítés után

\begin{matrix} f = \frac{2 a b}{b - a} sin \frac{γ}{2} = \frac{2 a b}{b - a} \sqrt[]{\frac{(s - a) (s - b)}{a b}} = \frac{2}{b - a} \sqrt[]{a b (s - a) (s - b)} . \end{matrix}

Böröczky György (Budapest, Madách I. g. IV. o. t.)

Megjegyzések. 1. A két szögfelezőszakasz egyenlősége meglepő, különösen azok részére, akik ismerik a következő tételt: a háromszög két belső szögfelezőjének a csúcs és a szemben levő oldal közé eső szakasza akkor és csak akkor egyenlő, ha a háromszög egyenlő szárú és a kérdéses felezők az egyenlő szögeket felezik. Kézenfekvő volna ebből az a sejtés, hogy két külső szögfelezőszakasz egyenlő voltából is következik, hogy a háromszög egyenlő szárú, láttuk azonban, hogy ez nem áll. Ezért szokás az ilyen háromszögeket pszeudo‐egyenlő szárú háromszögnek (magyarul ál‐egyenlő szárú) nevezni. Példánk is ilyen.
Az idézett tételnek az is érdekessége, hogy a fordított állítás bizonyítása ‐ ti. hogy ha két belső szögfelezőszakasz egyenlő hosszú, akkor a felezett szögek (ill. a szemben levő oldalak) egyenlők ‐ jóval nehezebb, mint az várható volna.
2. Abból a követelményből, hogy az

A

és

C

csúcsokból húzott külső szögfelezőszakaszok egyenlők legyenek, következik, hogy a háromszög oldalai között teljesülnie kell a következő egyenlőségnek:

\begin{matrix} b^{3} - (a + c) b^{2} + 3 a b c - a c (a + c) = 0. \end{matrix}

Horváth Péter (Budapest, Kossuth L. gépip. t. II. o. t.)

^{$^{*}$}Az ábrán

E

és

e

pótlandó.

^{$^{*}$}Vagy pedig $B E = e > 0$ , (2) helyére $c : (a - b) = (e - c) : b$ lép, és (3) negatívját kapjuk.