Feladat: 1153. matematika feladat Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Kotsis Domokos 
Füzet: 1962/november, 114 - 115. oldal  PDF  |  MathML 
Témakör(ök): Szerkesztések a térben, Feladat, Paralelepipedon
Hivatkozás(ok):Feladatok: 1962/január: 1153. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A P paralelepipedont megszerkesztettnek tekinthetjük, ha meghatároztuk mind a 6 lapsíkját. Ekkor bármelyik Σ lapsíkból a 4 vele nem párhuzamos lapsík kimetszi a Σ-n levő 4 élt, a 4 csúcsot pedig e 4 él közül a nem párhuzamos párok metszéspontja adja.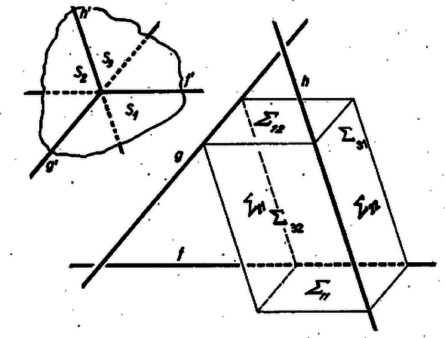

 
 

A test 12 éle 4-esével párhuzamos, ezért mindegyik adott egyenesünk másik 4-esbe tartozik, tehát f, g, h egyeneseinkkel megkaptuk P minden élének irányát. Belőlük a 3 párhuzamos lapsík pár állását is meghatározhatjuk, azaz egy‐egy olyan síkot, amely párhuzamos P-nek 2 szemközti lapjával. Evégett egy tetszés szerinti C ponton át meghúzzuk az f, g, h-val párhuzamos f', g', h' egyenest, ekkor az f', g', a g', h' és a h', f' metsző egyenes párok által meghatározott S1, S2, S3 síkok adják meg P lapsíkjainak állását. Magukat a lapsíkokat helyzet szerint rögzítve párosával úgy kapjuk, hogy vesszük az f-en, ill. g-n átmenő, S1-gyel párhuzamos Σ11, ill. Σ12 síkot, továbbá a g-n, ill. h-n átmenő, S2-vel párhuzamos Σ21, Σ22 síkot, végül az f-en, ill. h-n átmenő, S3-mal párhuzamos Σ31 Σ32 síkot.
Így a 6 páronként párhuzamos sík paralelepipedont határoz meg, és f, g, h mindegyikén 2 különböző állású Σ-sík megy át, tehát mindegyik egyenesünk a paralelepipedonnak éle. Szerkesztéseink egyértelműek, ezért ha van megoldás, akkor 1 megoldás van. Megoldás csak akkor nincs, ha valamelyik egyenesre illesztett 2 sík ‐ pl. az f-en átmenő Σ11 és Σ31 ‐, nem metszi egymást, hanem egybeesik. Ez ‐ a példát folytatva - azt jelenti, hogy már S1 és S3 is egybeesnek, tehát h' benne van S1-ben és ennélfogva S2 is egybeesik S1 és S3-mal, és így a g-n, ill. h-n átmenő 2‐2 sík is egybeesik. Ez azt jelenti, hogy van olyan sík, amely, f, g, h mindegyikével párhuzamos. (Pl. f, g, h különböző magasságban fekvő különböző irányú vízszintes egyenesek.)
 
 Kotsis Domokos (Budapest, József A. g. III. o. t.)
 
Megjegyzések. 1. Egyszerűbben kapjuk a lapsíkokat, ha mindegyik adott egyenesen át megszerkesztjük az egy‐egy további egyenessel párhuzamos síkot, pl. f-en át a g-vel, valamint a h-val párhuzamos síkot. A fenti módon viszont könnyebb belátni, hogy nincs mindig megoldás. Ennek vizsgálata számos dolgozatból hiányzik, másrészt gyakori az a téves megállapítás, hogy a feladatnak mindig van pontosan egy megoldása.
2. Több szorgalmas megoldó nem jól nézett utána a szükséges fogalmaknak. Így adódott pl, a következő kiindulás: ,,A paralelepipedon olyan poliéder, melynek határoló lapjai paralelogrammák; ebből következik, hogy szemközti határoló lapjai párhuzamosak és egybevágók''. Helyesen két‐két lap párhuzamosságát követeljük meg, és ennek lesz következménye a határoló lapok paralelogramma alakja és a szemben fekvő lapok egybevágósága, ‐ ha még azt is hozzávesszük, hogy a különböző állású sík‐párok száma 3 legyen. Az idézett kijelentés ráillik pl. a kristálytanból is ismert, 12 egybevágó rombusszal határolt ún. rombdodekaéderre is, amely kockából származtatható az 1078. feladatban1 leírt módon. Az idézet szerint két (,,valódi'') paralelepipedonból ‐ ha van egybevágó lapjuk ‐ az ezek mentén való összeillesztéssel előállott poliéder is paralelepipedon volna, és ezt az eljárást tovább akárhányszor ismételhetnénk.
Több dolgozat viszont feleslegesen hozzátette a meghatározó jegyekhez a szomszédos lapok merőlegességét. Ebben az értelemben azt is olvashattuk, hogy az adott egyenesek csak merőlegesek lehetnek.
Néhány versenyző előtt a térbeli szerkesztés fogalma nem volt világos: ,,elméletileg úgy oldom meg, hogy ..., de megszerkeszteni nem tudom, mert nem tanulok ábrázoló geometriát.'' A fenti megoldás példát mutatott egy térbeli szerkesztés elvégzésére.
1K. M. L. 23 (1961/11) 124. o.