Kezdőlap


Feladat:	1152. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baróti György , Bellay Ágnes , Benczúr András , Bokody andrea , Farkas Zoltán , Fazekas P. , Földes Antónia , Gálfi László , Kotsis D. , Kunszt Zoltán , Lehel J. , Nárai György , Raisz M. , Reuss P. , Sebestyén Zoltán , Seprődi László , Somogyi K. , Sonnevend György , Surányi A. , Szentai Judit , Szepesvári István , Szidarovszky Ágnes , Szidarovszky Ferenc , Varga L. , Vincze I. , Zalán Péter , Zalay M.
Füzet:	1962/december, 216 - 219. oldal		PDF \| MathML
Témakör(ök):	Műveletek helyvektorok koordinátáival, Egyenesek egyenlete, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1962/január: 1152. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A feladatot alkalmas koordinátarendszer bevezetésével oldjuk meg. Válasszuk tengelyekül az $O B$ , $O A$ egyeneseket úgy, hogy $B$ és $A$ a negatív féltengelyeken legyenek¹ és egységül a kör sugarát, tehát $A$ és $B$ koordinátái $(0; - 1)$ , ill. $(- 1; 0)$ . $P$ helyzetét az $O P$ sugár $φ$ forgásszögével határozzuk meg, a $Q$ és $R$ pontokét pedig koordinátáikkal. $P$ koordinátái ( $cos φ$ , $sin φ$ ); $P$ minden $A$ -tól és $B$ -től különböző helyzetét tekintetbe kell vennünk a körön, tehát 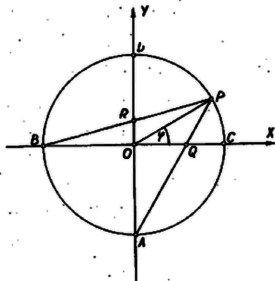$0^{\circ} \leq φ < 360^{\circ}$ , $φ \neq 180^{\circ}$ , $270^{\circ}$ .

1. ábra

Q

-t és

R

-et meghatározó egyenesek egyenlete:

\begin{matrix} P A : y + 1 = \frac{sin φ + 1}{cos φ} x (φ \neq 90^{\circ}), \\ O B : y = 0, \\ P B : y = \frac{sin φ}{cos φ + 1} (x + 1), \\ O A : x = 0, \end{matrix}

ennélfogva a pontok koordinátái, mint

φ

függvényei:

\begin{matrix} Q (\frac{cos φ}{sin φ + 1}, 0), ill. R (0, \frac{sin φ}{cos φ + 1}), \end{matrix}

és látható, hogy a

Q

abszcisszájára nyert képlet

φ = 90^{\circ}

mellett is érvényes.
Amíg

0^{\circ} \leq φ < 180^{\circ}

Q

befutja a

C B

átmérőt a

B

pont kivételével (

C

(1; 0)

pont), a

180^{\circ} < φ < 270^{\circ}

értékekre befutja az

O B

sugár

B

-n túli meghosszabbítását, végül a

270^{\circ} < φ < 360^{\circ}

értékekre az

O C

sugár

C

-n túli meghosszabbítását. Így ha

P

a III körnegyedben van,

Q

abszcisszája kisebb

- 1

-nél, egyébként nagyobb nála. ‐

R

viszont a

0^{\circ} \leq φ < 180^{\circ}

értékekre az

O D

félegyenest futja be (

D

(0; 1)

pont),

180^{\circ} < φ < 360^{\circ}

φ \neq 270^{\circ}

mellett pedig az

O

kezdetű,

A

-n átmenő félegyenest, fordított sorrendben, az

A

pont kivételével. Így ha

P

a III negyedben van,

R

ordinátája kisebb

- 1

-nél, egyébként nagyobb nála.
b) A

Q

és

R

közti kapcsolat megállapításához

Q

abszcisszája és

R

ordinátája között kell összefüggést keresnünk. Ehhez célszerű mindkettőt

φ

-nek egyetlen szögfüggvényével kifejezni, azután ezt a két kifejezésből kiküszöbölni. Erre a

t = tg φ / 2

kifejezés a legalkalmasabb (hacsak

φ / 2 \neq 90^{\circ}

, de ezt az értéket már kizártuk):

\begin{matrix} x_{Q} = x = \frac{\frac{1 - t^{2}}{1 + t^{2}}}{\frac{2 t}{1 + t^{2}} + 1} = \frac{1 - t^{2}}{1 + 2 t + t^{2}} = \frac{(1 + t) (1 - t)}{{(1 + t)}^{2}} = \frac{1 - t}{1 + t}, \end{matrix}

(1)

(mindig érvényes, mert a

t = - 1

φ / 2 = 135^{\circ}

értéket kizártuk) és

\begin{matrix} y_{R} = y = \frac{\frac{2 t}{1 + t^{2}}}{\frac{1 - t^{2}}{1 + t^{2}} + 1} = t . \end{matrix}

(1a)

t

kiküszöbölésével az

x

és

y

közötti keresett összefüggés:

\begin{matrix} x = \frac{1 - y}{1 + y}, másképpen y = \frac{1 - x}{1 + x} . \end{matrix}

(2)

Láttuk, hogy

Q

nem eshet

B

-be, ezért az

x = - 1

érték ki van zárva, tehát

x

minden értékéhez egy és csak egy

y

tartozik, azaz minden

Q

-hoz egy és csak egy

R

pont, a szerkesztő eljárásnak megfelelően. (2) így is írható:

\begin{matrix} (1 + x) (1 + y) = 2. \end{matrix}

(3)

2. ábra

B

C

A

D

P

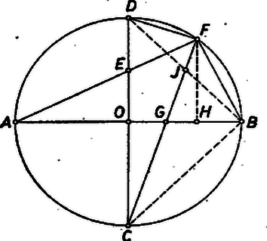pontunk szerepét átadva a 662. gyakorlat

A

B

C

D

, ill.

F

pontjának (2. ábra),

R

, ill.

Q

szerepét az ottani

E

, ill.

G

kapja és

\begin{matrix} tg \frac{φ}{2} = tg \frac{B O F ∢}{2} = tg B A F ∢ = \frac{O E}{A E} = \frac{1}{2}, \end{matrix}

tehát a 662. gyakorlat b) részében feladatunknak egy határozott

φ

értékkel adódó esetét vizsgáltuk. Ezzel (1) alapján, az ottani eredménnyel megegyezésben:

\begin{matrix} O G = O Q = \frac{1 / 2}{3 / 2} = \frac{1}{3}, 3 O G = 1 = O B . \end{matrix}

d) Az

A B Q R

négyszög a

0^{\circ} < φ < 90^{\circ}

értékekre hurkolt (1. ábra), területe nincs értelmezve. A

90^{\circ} \leq φ < 180^{\circ}

és

270^{\circ} < φ < 360^{\circ}

értékekre a terület az

A B O

és

Q R O

háromszögek területének összege (3‐4. ábrák):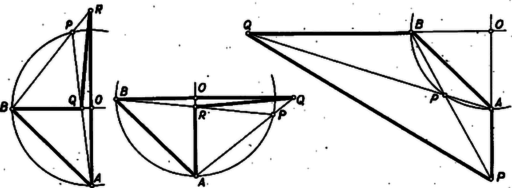

\begin{matrix} T = \frac{1}{2} + \frac{| x | \cdot y}{2}, ill. T = \frac{1}{2} + \frac{x \cdot | y |}{2} . \end{matrix}

\begin{matrix} 3. ábra,                 4. ábra,                      5.  ábra \end{matrix}

Az első intervallumon végighaladva

| x |

és

| y |

növekednek, a másodikon végighaladva

x

és

| y |

fogynak, így

T

nem állandó. Végül a

180^{\circ} < φ < 270^{\circ}

intervallumban (5. ábra, az alsó

P

pont helyesen

R

\begin{matrix} T = Q R O - A B O = \frac{1}{2} | x | \cdot | y | - \frac{1}{2} = \frac{- x}{2} \cdot \frac{1 - x}{- 1 - x} - \frac{1}{2} = \\ = - \frac{x^{2} + 1}{2 (x + 1)} = \frac{1 - x}{2} - \frac{1}{x + 1}, \end{matrix}

ugyanis ‐ mint fent megjegyeztük ‐ itt mindig

x < - 1

y < - 1

, ezért

| x | = - x

, (2)-ben

y

számlálója pozitív, nevezője negatív. Az utolsó alak első tagja elsőfokú függvény, második tagja elsőfokú törtfüggvény, képük egyenes, ill. hiperbola, így a

T

értékét megadó függvény képe nem egyenes,

T

értéke itt sem állandó.
(Az

A B R Q

négyszög területe viszont a

180^{\circ} < φ < 270^{\circ}

intervallum kivételével állandó, mert átlói,

B Q

és

A R

merőlegesek, hosszuk

1 + x

, ill.

1 + y

‐ a fentiek szerint pozitívok ‐ és így (3) felhasználásával

\begin{matrix} T = \frac{1}{2} \cdot B Q \cdot A R = \frac{1}{2} (1 + x) (1 + y) = 1. \end{matrix}

180^{\circ} < φ < 270^{\circ}

értékekre az

A B R Q

négyszög hurkolt.)

Kunszt Zoltán (Pápa, Türr I. g. IV. o. t.)

Megjegyzés. Amíg

φ < 180^{\circ}

O R

értékét az

R B O

derékszögű háromszögből a kerületi szög tételének felhasználásával is egyszerűen kapjuk. Így ugyanis

R

mindig az

O D

félegyenesen van, ezért

\begin{matrix} R B O ∢ = P B C ∢ = \frac{P O C ∢}{2} = \frac{φ}{2}, O R = B O tg R B O ∢ = tg \frac{φ}{2} = t . \end{matrix}

Míg

φ

180^{\circ}

-tól

360^{\circ}

-ig növekszik ‐ vagy ami ugyanaz,

- 180^{\circ}

-tól

0^{\circ}

-ig ‐, csak annyi a változás, hogy

O R

negatívját kell vennünk, mert a

B A C

félkör a

B D C

félkör tükörképe az

X

-tengelyre nézve. Kifejezésünk tehát helyes, mert egy szög tangensének negatívja egyenlő a szög negatívjának tangensével.
Hasonlóan látható be, hogy a

Q A O

háromszögből nyert

\begin{matrix} O Q & = A O tg Q A O ∢ = tg P A D ∢ = tg \frac{P O D ∢}{2} = tg \frac{90^{\circ} - φ}{2} = \\ = tg (45^{\circ} - \frac{φ}{2}) = \frac{1 - tg \frac{φ}{2}}{1 + tg \frac{φ}{2}} = \frac{1 - t}{1 + t} \end{matrix}

kifejezés is mindig helyes.

¹Ezzel a választással egyszerűbb lesz a 662. gyakorlattal való összehasonlítás.