Kezdőlap


Feladat:	1150. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aradi J. , Baróti György , Benczúr András , Bodoky Andrea , Demendy Z. , Farkas Zoltán , Földes Antónia , Földes Iván , Gálfi László , Gerencsér László , Gyárfás András , Horváth P. , Horváth Péter , Kármán A. , Kobzos L. , Kotsis D. , Kunszt Zoltán , László Erika , Lehel Jenő , Magyar Erzsébet , Nárai Gy. , Nováky Béla , Opálény M. , Pázmándi László , Rozváczy Judit , Sebestyén Zoltán , Seprődi László , Simonovits Miklós , Sonnevend György , Surányi András , Szabó László , Szepesvári I. , Szidarovszky Ágnes , Szidarovszky Ferenc , Szigeti F. , Tamás Endre , Vágvölgyi Györgyi , Varga L. , Vesztergombi György , Vincze I. , Zalán Péter
Füzet:	1963/március, 109 - 113. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Diszkusszió, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1962/január: 1150. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Szerkesztéssel az alábbiak szerint kaphatjuk a keresett $A_{1}$ pontot. Legyen $B^{*}$ az $A C$ egyenes tetszés szerinti, $A$ -tól különböző pontja, $C^{*}$ ennek merőleges vetülete az $A B$ egyenesen, továbbá a $B^{*}$ -ból $A C$ -re és $C^{*}$ -ból $B C$ -re állított merőleges egyenesek metszéspontja $A^{*}$ . Ekkor $A_{1}$ az $A A^{*}$ egyenesnek $B C$ -vel való metszéspontja.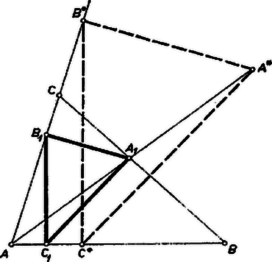

1. ábra

Jelöljük ugyanis

A_{1}

vetületét

C A

-ra

B_{1}

-gyel,

B_{1}

vetületét

A B

-re

C_{1}

-gyel. Ekkor

A_{1} B_{1} ∥ A^{*} B^{*}

és

B_{1} C_{1} ∥ B^{*} C^{*}

, s így

A A_{1} B_{1}

és

A A^{*} B^{*}

, továbbá

A B_{1} C_{1}

és

A B^{*} C^{*}

hasonló háromszögpárok. Ezekből

\begin{matrix} \frac{A A_{1}}{A A^{*}} = \frac{A B_{1}}{A B^{*}} és \frac{A B_{1}}{A B^{*}} = \frac{A C_{1}}{A C^{*}}, \end{matrix}

\begin{matrix} s így \frac{A A_{1}}{A A^{*}} = \frac{A C_{1}}{A C^{*}} . \end{matrix}

Ebből viszont következik az

A A_{1} C_{1}

és

A A^{*} C^{*}

háromszögek hasonlósága, mert egy szögük közös és az ezt bezáró oldalak aránya egyenlő. Ennek folytán

A_{1} C_{1} ∥ A^{*} C^{*}

tehát

A_{1} C_{1} ⊥ B C

A^{*}

mindig létrejön és

A

-tól különböző, mert a

B^{*}

-ban

A C

-re állított merőleges nem megy át

A

-n és nem párhuzamos a

C^{*}

-ból

B C

-re állított merőlegessel.
Másrészt az

A_{1}

csúcs (és vele együtt a többi is) egyértelműen meg van határozva, mert ha egy

A_{1} B_{1} C_{1}

háromszög megfelel a feladat feltételeinek, akkor egy

A

középpontú hasonlósági transzformációval

B_{1}

csúcsa átvihető

B^{*}

-ba; ekkor azonban az egész háromszög az

A^{*} B^{*} C^{*}

háromszögbe kell, hogy átmenjen, s így

A_{1}

csak az

A A^{*}

egyenesen (és másrészt a

B C

oldalon) lehet.
Ugyanígy szerkeszthetünk a

B C

egyenes egy pontjából kiindulva ‐ az

A

és

B

csúcsok szerepének felcserélésével ‐ egy háromszöget, melyből

B

középpontú hasonlósági transzformációval kapható az

A_{2} B_{2} C_{2}

háromszög, és ez is egyértelműen meg van határozva.
Tükrözzük az

A_{1} B_{1} C_{1}

háromszöget a köréje írt

k_{1}

kör

O_{1}

középpontjára nézve, és legyen a csúcsok képe rendre

A'_{1}

B'_{1}

C'_{1}

. Megmutatjuk, hogy ezek egybeesnek a

B_{2}

C_{2}

A_{2}

pontokkal.

C'_{1}

B C

egyenesen van, mert rajta van

k_{1}

-en, így a

C'_{1} A_{1} C_{1}

szög derékszög, tehát a

C'_{1} A_{1}

egyenes azonos

B C

-vel. Ugyanígy

A'_{1}

C A

egyenesen,

B'_{1}

pedig

A B

-n van rajta.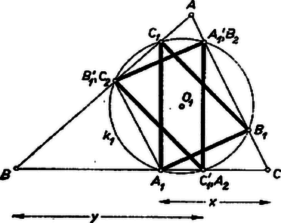

2. ábra

A'_{1} B'_{1} C'_{1}

háromszög oldalai párhuzamosak az

A_{1} B_{1} C_{1}

háromszög megfelelő oldalaival, tehát rendre merőlegesek az

A B C

háromszög egy-egy oldalára (2. ábra):

\begin{matrix} C'_{1} B'_{1} ∥ C_{1} B_{1} ⊥ B A, B'_{1} A'_{1} ∥ B_{1} A_{1} ⊥ A C, \end{matrix}

\begin{matrix} A'_{1} C'_{1} ∥ A_{1} C_{1} ⊥ C B . \end{matrix}

Eszerint a

C'_{1}

A'_{1}

B'_{1}

pontoknak rendre megvan az a tulajdonsága, amelyet

A_{2}

B_{2}

C_{2}

-től kívánunk. Ámde láttuk, hogy

A_{2}

B_{2}

C_{2}

a követelményekkel egyértelműen meg van határozva, tehát az

A_{2} B_{2} C_{2}

háromszög azonos a

C'_{1} A'_{1} B'_{1}

háromszöggel és ‐ azonos körüljárással ‐ egybevágó annak az

O_{1}

pontra vonatkozó

C_{1} A_{1} B_{1}

tükörképével.
Ezzel az állítást bebizonyítottuk, egyszersmind a feladatban kimondott egybevágóságban a csúcsok megfelelő párjait is megállapítottuk.

Lehel Jenő (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

II. megoldás. Származtathatjuk az

A_{1} B_{1} C_{1}

és az

A_{2} B_{2} C_{2}

háromszöget is egy-egy olyan háromszög kicsinyítésével, amelynek

A B

-re merőleges oldala a

C C^{*}

magasság. Legyen a

C

-n át

A C

-re és

C^{*}

-on át

B C

-re merőlegesen húzott egyenesek metszéspontja

A^{*}

, a

C

-n át

B C

-re és

C^{*}

-on át

A C

-re merőlegesen húzott egyeneseké pedig

B^{*}

. Ekkor

A_{1}

-et az

A A^{*}

egyenes metszi ki

B C

-ből,

B_{2}

-t pedig a

B B^{*}

egyenes

A C

-ből. Ezekből a pontokból megrajzolva az

A_{1} B_{1} C_{1}

, ill.

A_{2} B_{2} C_{2}

háromszöget, ezek megfelelnek a feladat követelményeinek, és csak egy-egy ilyen háromszög létezik, amint azt az I. megoldásban beláttuk.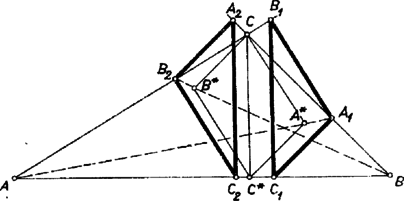

3. ábra

Ez a két háromszög az egymással egybevágó

A^{*} C C^{*}

, ill.

B^{*} C^{*} C

háromszögből hasonlósági transzformációval keletkezett, a hasonlóság aránya

A A_{1} / A A^{*}

, ill.

B B_{2} / B B^{*}

. Így az

A_{1} B_{1} C_{1}

és

A_{2} B_{2} C_{2}

háromszög egybevágó volta következik abból, ha bebizonyítjuk e két arány egyenlőségét. Evégett megmutatjuk, hogy

A A^{*} C

és

B B^{*} C

hasonló háromszögek és

C A_{1}

C B_{2}

bennük egymásnak megfelelő egyenesek.
Mivel az

A^{*} C C^{*}

háromszög oldalai merőlegesek a

C A B

háromszög megfelelő oldalaira, így a két háromszög hasonló, és ebből

\begin{matrix} \frac{A^{*} C}{C A} = \frac{A^{*} C^{*}}{C B} = \frac{B^{*} C}{C B} . \end{matrix}

A A^{*} C

és

B B^{*} C

háromszögekben tehát, melyek

C

-nél derékszögűek, a befogók aránya megegyezik, s így a két háromszög hasonló.
Az

A_{1} C

egyenesnek a

C A^{*}

befogóval és a

B_{2} C

egyenesnek a

C B^{*}

befogóval bezárt szöge egyaránt az

A C B

szög eltérése

90^{\circ}

-tól.

A_{1}

is,

B_{2}

is a megfelelő átfogó pontja, ha

A C B ∢ ≦ 90^{\circ}

, és az átfogók

A^{*}

-on, ill.

B^{*}

-on túli meghosszabbítására esnek, ha

A C B ∢ > 90^{\circ}

. Így

C A_{1}

és

C B_{2}

a két hasonló derékszögű háromszögre nézve egymásnak megfelelő szakaszok, ennélfogva

A A_{1} / A A^{*} = B B_{2} / B B^{*}

, és ezt akartuk bizonyítani.

Szidarovszky Ferenc (Budapest, Fazekas M. gyak. g. III. o. t.)

III. megoldás. Szerkesszünk meg egy

A^{*} B^{*} C^{*}

háromszöget, mint az I. megoldásban, és legyen

A^{*}

tükörképe

B^{*} C^{*}

középpontjára

A^{*}'

. Ekkor az

A^{*}' B^{*} C^{*}

háromszög oldalai rendre a

C B

B A

A C

oldalakra merőlegesek, ugyanúgy, mint azt a

B_{2} A_{2} C_{2}

háromszög egymás utáni oldalaitól kívánja a feladat. Ha ezt a háromszöget még eltoljuk az

A B

egyenessel párhuzamosan úgy, hogy

A^{*}'

A C

oldalra kerüljön, akkor a keletkező

A' B' C'

háromszöget

A

középpontú hasonlósági transzformáció viszi át

B_{2} A_{2} C_{2}

-be, hasonlóan, mint az

A^{*} B^{*} C^{*}

háromszöget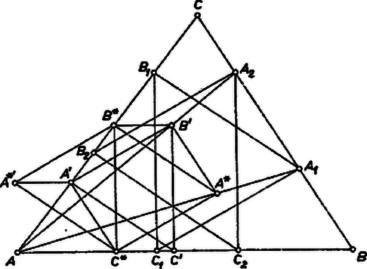

A_{1} B_{1} C_{1}

-be.

4. ábra

Azt kell még megmutatnunk, hogy a két esetben ugyanazt a hasonlósági transzformációt kell alkalmazni. Ez következik abból, ha megmutatjuk, hogy

A^{*} B' ∥ B C

, mert a hasonlósági transzformáció minden egyenest vele párhuzamos egyenesbe visz át, tehát az említett párhuzamosság esetén az

A^{*}

-ot

A_{1}

-be átvivő transzformáció

B'

-t is a

B C

egyenesen levő pontba viszi át.
A kívánt párhuzamosság viszont következik abból, ha megmutatjuk, hogy

A' C^{*} ∥ B C

, vagyis az

A C^{*} A'

és

A B C

háromszögek hasonlók, mert

A^{*} C^{*}

és

B' A'

párhuzamos és egyenlő szakaszok, tehát

A^{*} B' A' C^{*}

paralelogramma.
Az

A A' C'

és

A B^{*} C^{*}

háromszögek hasonlók, mert mindkettő derékszögű és

A

-nál levő szögük közös, vagy az egyik a másiknak csúcsszöge (ha a

B A C

szög tompaszög). Így

A A' / A C^{*} = A' C' / C^{*} B^{*}

. De

A' C' = B^{*} A^{*}

és

B^{*} A^{*} / C^{*} B^{*} = A C / B A

, mert az

A^{*} B^{*} C^{*}

és a

C A B

háromszög megfelelő oldalai egymásra merőlegesek, s így a háromszögek hasonlók.
Azt kaptuk tehát, hogy az

A B C

és

A C^{*} A'

háromszögekben, amelyeknek az

A

-nál levő szögei egybeesnek vagy csúcsszögek, az ezt közrefogó, megfelelő oldalak aránya megegyezik. Így

A' C^{*} ∥ C B

. Mint láttuk, ebből következik, hogy az

A B C

háromszögbe lehet beírni két egybevágó háromszöget, melyeknek oldalai merőlegesek az előírt sorrendben az

A B C

háromszög oldalaira. Mivel az előírásoknak megfelelő háromszögek egyértelműen meg vannak határozva ‐ lásd az I. megoldást ‐, így a feladat állítása bizonyítást nyert.

IV. megoldás.

A_{1}

és

A_{2}

helyzetét számítással is meghatározhatjuk a háromszög (szokás szerint jelölendő) oldalaiból és szögeiből. Legyen

C A_{1} = x

, a

C

-ből

B

felé mutató irányt véve pozitívnak. (A

B_{1}

C_{1}

A_{2}

B_{2}

C_{2}

csúcsokat is az

A B C

háromszög megfelelő két csúcsától mért távolságukkal határozzuk meg, pozitívnak mindig a szóban forgó oldal másik végpontja felé mutató irányt vesszük.) Ebből, a koszinuszokat természetesen előjellel értve (2. ábra):

\begin{matrix} C B_{1} = x cos γ, A B_{1} = b - x cos γ, A C_{1} = b cos α - x cos α cos γ, \end{matrix}

\begin{matrix} B C_{1} = c - b cos α + x cos α cos γ = a cos β + x cos α cos γ \end{matrix}

(felhasználtuk a

b cos α + a cos β = c

összefüggést). Most már a követelmény figyelembevételével

\begin{matrix} B A_{1} = B C_{1} cos β = a cos^{2} β + x cos α cos β cos γ = a - x, és így \end{matrix}

\begin{matrix} x = \frac{a sin^{2} β}{1 + cos α cos β cos γ} . \end{matrix}

Hasonlóan

B A_{2} = y

-nal kifejezve rendre a

B C_{2}

A C_{2}

A B_{2}

C B_{2}

szakaszt, felhasználva a

c cos α + a cos γ = b

összefüggést, a

C A_{2} = a - y = C B_{2} cos γ

követelményből

\begin{matrix} y = \frac{a sin^{2} γ}{1 + cos α cos β cos γ} . \end{matrix}

Így

x

és

y

, ill.

A_{1}

és

A_{2}

, ill. velük az

A_{1} B_{1} C_{1}

és

A_{2} B_{2} C_{2}

háromszögek mindig egyértelműen meg vannak határozva, mert a nevező sohasem 0, ugyanis a koszinuszok szorzata abszolút értékben kisebb 1-nél.
A kérdéses egybevágóság most már következik abból, ha megmutatjuk, hogy a

B_{1} C_{1} A_{1}

és

C_{2} A_{2} B_{2}

háromszögekben ‐ melyeknek szögei rendre egyenlőek az

A B C

háromszög szögeivel, és így hasonlók egymáshoz ‐, egy pár megfelelő oldal egyenlő. Az első háromszögnek az

A_{1} C_{1} B_{1} = β

szöggel szemben fekvő oldala a szinusz tétel felhasználásával

\begin{matrix} A_{1} B_{1} = x sin γ = \frac{a sin^{2} β sin γ}{1 + cos α cos β cos γ} = \frac{b sin α sin β sin γ}{1 + cos α cos β cos γ} . \end{matrix}

Hasonlóan

\begin{matrix} A_{2} C_{2} = y sin β = \frac{c sin α sin γ sin β}{1 + cos α cos β cos γ} . \end{matrix}

A második háromszögben a szinusz tétel alapján

\begin{matrix} \frac{B_{2} C_{2}}{A_{2} C_{2}} = \frac{sin B_{2} A_{2} C_{2} ∢}{sin A_{2} B_{2} C_{2} ∢} = \frac{sin β}{sin γ} = \frac{b}{c}, \end{matrix}

és így

\begin{matrix} B_{2} C_{2} = \frac{b}{c} \cdot A_{2} C_{2} = A_{1} B_{1}, \end{matrix}

ami állításunkat igazolja.

Gálfi László (Budapest, I. István g. IV. o. t.)