Kezdőlap


Feladat:	1146. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ámon Magdolna , Bán Tamás , Baróti György , Berecz Ágota , Dobó F. , Fajszi Cs. , Farkas Zoltán , Fejéregyházi S. , Gács I. , Gálfi László , Ghihor Zoltán , Horváth Kálmán , Jójárt István , Kászonyi László , Kiss Ildikó , Kobzos L. , Kotsis D. , Kunszt Zoltán , Lánc József , Lehel J. , Magyar Erzsébet , Malatinszky G. , Minkó B. , Nagy Dénes L. , Nagy Ernő , Nováky Béla , Opálény M. , Parragh Zoltán , Reuss Pál , Sebestyén Zoltán , Seprődi László , Simenszky Csilla , Simonovits Miklós , Somogyi K. , Sonnevend György , Surányi Andor , Szekeres Veronika , Szidarovszky Ferenc , Tamás E. , Tamás G. , Tungler A. , Varga L. , Vesztergombi György , Vincze I. , Zalán F. Á. , Zalán Péter , Zalay M.
Füzet:	1962/november, 108 - 109. oldal		PDF \| MathML
Témakör(ök):	Gömbi geometria, Feladat
Hivatkozás(ok):	Feladatok: 1961/december: 1146. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I.^* A csillagászati földrajzból tudjuk, hogy dec. 22-én, márc. 21-én, jún. 22-én és szept. 23-án a Nap rendre a Baktéritőre, az Egyenlítőre, a Ráktérítőre, ill. ismét az Egyenlítőre süt merőlegesen (a tett egyszerűsítések szellemében feltehetjük, hogy a mondott dátumokon az egész napon át), ennélfogva a keresett helyek földrajzi szélessége rendre $φ_{1} = - 23, 5^{\circ}$ , $φ_{2} = 0^{\circ}$ , $φ_{3} = 23, 5^{\circ}$ , $φ_{4} = 0^{\circ}$ .
Másrészt bármely helyen napkeltekor és napnyugtakor a napsugarak $0^{\circ}$ szögben érik az illető hely vízszintes síkját, a kérdéses helyeken viszont $90^{\circ}$ szögben, ezért a kérdéses helyeket Budapesttel összekötő legrövidebb ívekhez (főkörívekhez) a Föld középpontjában $ϑ = 90^{\circ}$ -os középponti szög tartozik. Ennélfogva a $P_{0} (λ_{0}, φ_{0})$ és $P_{i} (λ_{i}, φ_{i})$ földrajzi koordinátákkal meghatározott helyeknek főköríven mért $ϑ$ szögtávolságára fent idézett képletben $cos ϑ = 0$ , és így

\begin{matrix} cos (λ_{0} - λ_{i}) = - tg φ_{0} tg φ_{i} . \end{matrix}

(1)

Vegyük

P_{0}

-nak mindvégig Budapestet, így

λ_{0} = + 19, 1^{\circ}

φ_{0} = 47, 5^{\circ}

P_{i}

-nek pedig rendre a keresett pontokat.

φ_{1} = - 23, 5^{\circ}

-kal

\begin{matrix} cos (λ_{0} - λ_{1}) = 1, 091 \cdot 0, 4348 = 0, 4745, \\ λ_{0} - λ_{1} = \pm 61, 7^{\circ}, tehát λ'_{1} = + 80, 8^{\circ}, λ''_{1} = - 42, 6^{\circ} . \end{matrix}

P''_{1}

(

λ''_{1}

φ_{1}

) pont Rio de Janeiro (Brazília) közelében fekszik, ennek zenitjében áll a Nap dec. 22-én a budapesti napnyugta időpontjában; a

P'_{1}

(

λ'_{1}

φ_{1}

) pont pedig az Indiai óceánban, Ceylon délkörén, kb. a félúton Madagaszkár keleti és Ausztrália nyugati partja között (a budapesti napkeltekor). ‐ Hasonlóan

φ_{3}

-mal

\begin{matrix} cos (λ_{0} - λ_{3}) = - 0, 4745, λ_{0} - λ_{3} = \pm 118, 3^{\circ}, λ'_{3} = + 137, 4^{\circ}, λ''_{3} = 99, 2^{\circ}, \end{matrix}

P''_{3}

(

λ''_{3}

φ_{3}

) hely Mexikóban, Ciudad Victoria várostól délre fekszik (jún. 22, Bp. napnyugta), a

P'_{3}

(

λ'_{3}

φ_{3}

) hely pedig Tokiótól (Japán) délre és Tajvantól keletre (napkeltekor).
Nyilvánvaló, hogy márc. 21-én és szept. 23-án ugyanaz a két hely felel meg, ezekre

tg φ_{2} = 0

cos (λ_{0} - λ_{2}) = 0

λ_{0} - λ_{2} = \pm 90^{\circ}

λ'_{2} = + 109, 1^{\circ}

λ''_{2} = - 70, 9^{\circ}

. A

P'_{2} (λ'_{2}, φ_{2})

hely Indonéziában, Kalimantan (Borneo) szigetén, Pontianak város közelében fekszik (Bp. napkelte),

P''_{2} (λ''_{2}, φ_{2})

pedig Kolumbia és Brazília határán (napnyugta).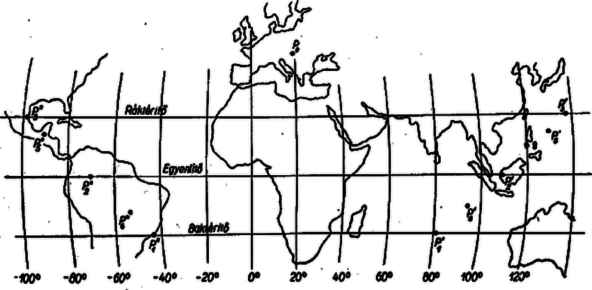

II. Ha a napsugarak délben Budapesten

60^{\circ}

-os szögben érik a vízszintest, akkor a Napnak a zenittől mért szögtávolsága

90^{\circ} - 60^{\circ} = 30^{\circ}

, ezért a Nap Budapest délkörének

φ_{5} = φ_{0} - 30^{\circ} = 17, 5^{\circ}

szélességű pontja fölött áll, és aznap egész napon át közelítőleg a

φ_{5}

-höz tartozó szélességi kör valamely pontjára süt merőlegesen. Ilyen hely van, mert

φ_{5}

- 23, 5^{\circ}

és

+ 23, 5^{\circ}

közé esik. A délben

30^{\circ}

-os szöget mutató napokon hasonlóan a

φ_{6} = 47, 5^{\circ} - 60^{\circ} = - 12, 5^{\circ}

szélességű helyekre süt merőlegesen a Nap, ilyen helyek is vannak. Most már (1)-ből

\begin{matrix} \begin{matrix} cos (λ_{0} - λ_{5}) = - 0, 3441, & cos (λ_{0} - λ_{6}) = + 0, 2419, \\ λ_{0} - λ_{5} = \pm 110, 1^{\circ}, & λ_{0} - λ_{6} = \pm 76, 0^{\circ}, \\ λ'_{5} = + 129, 2^{\circ}, λ''_{5} = - 91, 0^{\circ}, & λ'_{6} = + 95, 1^{\circ}, λ''_{6} = - 56, 9^{\circ} . \end{matrix} \end{matrix}

P_{5} (λ'_{5}, φ_{5})

hely a Fülöp szigetektől keletre, a

P'_{6} (λ'_{6}, φ_{0})

hely Jakartától délnyugatra fekszik (Bp. napkelte), végül a

P''_{6} (λ''_{6}, φ_{6})

hely Guatemala és Mexikó határán, a

P''_{5} (λ''_{5}, φ_{5})

hely pedig Brazíliának Mato Grosso tagállamában, Diamantino város közelében (bpesti napnyugta).

Reuss Pál (Budapest, József A. g. IV. o. t.)

^*Használhatjuk a (

λ_{1}, φ_{1}

) és (

λ_{2}, φ_{2}

) földrajzi helyeknek a gömbi főkörön mért

ϑ

szögtávolságára a K. M. L. 22 (1961/4) 157.-158. oldalon, az 1045. feladatban levezetett következő tételt:

\begin{matrix} cos ϑ = sin φ_{1} sin φ_{2} + cos φ_{1} cos φ_{2} cos (λ_{1} - λ_{2}) \end{matrix}