Kezdőlap


Feladat:	1145. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aleva Gy. , Baróti György , Bellay Ágnes , Benczúr András , Bokody andrea , Csűrös M. , Demendy Z. , Fajszi Cs. , Farkas Zoltán , Fejéregyházi S. , Fekete T. , Fodor J. , Gálfi László , Garai G. , Garai Gábor , Ghihor Zoltán , Horváth K. , Huber T. , Kiss Ildikó , Kóta J. , Kunszt Zoltán , Lánc József , László Erika , Lehel J. , Magyar Erzsébet , Máté Attila , Máté Eörs , Nagy Ernő , Nagy Géza , Négyessy M. , Nováky Béla , Oberländer V. , Opálény M. , Parragh Z. , Pór András , Pusztai T. , Raisz M. , Reuss P. , Sebestyén Zoltán , Seprődi László , Simonovits Miklós , Sonnevend György , Surányi Andor , Szentai Judit , Szepesvári I. , Szidarovszky Ágnes , Szidarovszky Ferenc , Szirai J. , Timár Gy. , Varga L. , Vesztergombi György , Vincze I. , Zalán P. , Zalay M.
Füzet:	1962/november, 107 - 108. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Terület, felszín, Koszinusztétel alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1961/december: 1145. matematika feladat

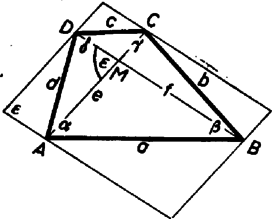
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyenek az ABCD négyszög oldalai $A B = a$ , $B C = b$ , $C D = c$ , $D A = d$ , egyik átlója $B D = f$ , az ezzel szemben levő szögek $B A D ∢ = α$ , $B C D ∢ = γ$ , végül a területe $t$ .

A B D

és

C B D

háromszögekből a

B D

átlóra és a négyszög 4-szeres területére

\begin{matrix} f^{2} = a^{2} + d^{2} - 2 a d cos α = b^{2} + c^{2} - 2 b c cos γ, & (1) \\ 2 a d sin α + 2 b c sin γ = 4 t . & (2) \end{matrix}

Átrendezéssel (1)-ből

\begin{matrix} 2 a d cos α - 2 b c cos γ = a^{2} + d^{2} - b^{2} - c^{2} . \end{matrix}

(3)

Képezzük (2) és (3) négyzetösszegét, mindjárt figyelembe véve a

\begin{matrix} sin^{2} x + cos^{2} x = 1 és cos x cos y - sin x sin y = cos (x + y) azonosságokat : \end{matrix}

\begin{matrix} 4 a^{2} d^{2} + 4 b^{2} c^{2} - 8 a b c d cos (α + γ) = 16 t^{2} + {(a^{2} + d^{2} - b^{2} - c^{2})}^{2} . \end{matrix}

Innen

\begin{matrix} 16 t^{2} = 4 a^{2} d^{2} + 4 b^{2} c^{2} - {[(a^{2} + d^{2}) - (b^{2} + c^{2})]}^{2} - 8 a b c d cos (α + γ) \end{matrix}

(4)

Adott

a

b

c

d

mellett a jobb oldal első 3 tagja állandó, ezért

16 t^{2}

és vele

t

akkor a legnagyobb, ha az utolsó tag a legnagyobb; ez pedig akkor áll be, ha

cos (α + γ)

a lehető legkisebb értékét,

- 1

-et veszi fel. Ekkor

\begin{matrix} 16 t_{max}^{2} = 256 + 1296 - {[65 - 45]}^{2} + 1152 = 2304, \end{matrix}

ahonnan

t_{max} = 12

területegység, hacsak létezik olyan négyszög, melynek egymás utáni oldalai az adott szakaszok, továbbá, amelyben a

cos (α + γ) = - 1

, azaz

α + γ = 180^{\circ}

kiegészítő feltétel is teljesül. Ekkor

cos γ = - cos α

, és így (3)-ból, majd (1)-ből

\begin{matrix} cos α = \frac{a^{2} + d^{2} - b^{2} - c^{2}}{2 (a d + b c)} = \frac{5}{13}, f \approx 7, 671 egység . \end{matrix}

Ez mind az

a

d

, mind a

b

c

oldalpárral háromszöget alkot, tehát a kérdéses négyszög létezik.
Azt is látjuk a szög‐feltételből, hogy négyszögünk húrnégyszög, és hogy bármely

a

b

c

d

oldalhosszak mellett ‐ ha egyáltalán létezik a négyszög ‐ a húrnégyszögnek van maximális területe.

II. (4) jobb oldalát a

cos (α + γ) = - 1

feltétel mellett kifejtve

\begin{matrix} 16 t_{max}^{2} = 2 (a^{2} b^{2} + a^{2} c^{2} + a^{2} d^{2} + b^{2} c^{2} + b^{2} d^{2} + c^{2} d^{2}) - \\ - (a^{4} + b^{4} + c^{4} + d^{4}) + 8 a b c d . \end{matrix}

Ebben a kifejezésben

a

b

c

d

mindegyike egyforma szerepet játszik, eszerint

t_{max}

értéke független az oldalak sorrendjétől (természetesen ismét számadatainktól is függetlenül).

Bellay Ágnes (Budapest, Fazekas M. gyak. g. IV. o. t.)

^*(4)-et a K. M. L. 23 (1961/11) 132. o. aljáról készen átvehettük volna, azonban új olvasóinkra tekintettel inkább levezettük.