Kezdőlap


Feladat:	1144. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Koplányi Erzsébet , Lippai Pál , Parragh Zoltán , Udvardy Antal
Füzet:	1962/október, 75 - 76. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1961/december: 1144. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A bal oldali hányadosnak minden (valóságos) háromszögben van értelme, mert a nevező sohasem 0. Ugyanis a koszinusz függvény ( $0^{\circ}$ -tól $180^{\circ}$ -ig) csökkenő, tehát

\begin{matrix} cos α + cos β > cos α + cos (β + γ) = cos α + cos (180^{\circ} - α) = 0. \end{matrix}

A feltevésből átszorzással és 0-ra redukálással

\begin{matrix} sin α + sin β - sin γ (cos α + cos β) = 0. \end{matrix}

Innen

sin γ = sin [180^{\circ} - (α + β)] = sin (α + β) = sin α cos β + cos α sin β

beírásával, a négyzetes összefüggés alapján, majd szorzattá alakítással

(sin α + sin β) - sin α cos β - cos^{2} α sin β - sin α cos^{2} β - cos α sin β cos β = (sin α + sin β) (1 - cos α cos β) - (1 - sin^{2} α) sin β - sin α (1 - sin^{2} β) = (sin α + sin β) (- cos α cos β + sin α sin β) = - (sin α + sin β) \cdot cos (α + β) = 0

.

Mivel

sin α + sin β

mindkét tagja pozitív, tehát összegük

\neq 0

, azért innen

cos (α + β) = 0

, azaz

α + β = 90^{\circ}

, az állításnak megfelelően. Eszerint a

γ

szög derékszög.

Koplányi Erzsébet (Budapest, Zrínyi I. lg. II. o. t.)

II. megoldás. (1) bal oldalán a számlálót és a nevezőt szorzattá alakítva, a jobb oldalon pedig a

sin x = 2 sin x / 2 cos x / 2

azonosság alapján:

\begin{matrix} \frac{sin α + sin β}{cos α + cos β} = \frac{2 sin \frac{α + β}{2} cos \frac{α - β}{2}}{2 cos \frac{α + β}{2} cos \frac{α - β}{2}} = \frac{sin \frac{α + β}{2}}{cos \frac{α + β}{2}}, \\ sin γ = sin (α + β) = 2 sin \frac{α + β}{2} cos \frac{α + β}{2} . \end{matrix}

A kapott két kifejezés egyenlőségéből, a 0-tól különböző számlálóval egyszerűsítve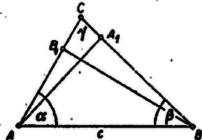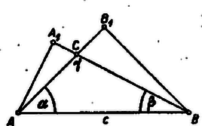

\begin{matrix} cos^{2} \frac{α + β}{2} = \frac{1}{2}, cos \frac{α + β}{2} = \frac{1}{\sqrt[]{2}}, \frac{α + β}{2} = 45^{\circ}, α + β = 90^{\circ}, \end{matrix}

ugyanis

α + β < 180^{\circ}

(α + β) / 2 < 90^{\circ}

, tehát koszinusza pozitív.

Udvardy Antal (Budapest, Táncsics M. g. III. o. t.)

III. megoldás. Megmutatjuk, hogy ha

γ

hegyesszög, vagy ha tompaszög, akkor a feltevés nem teljesülhet. Rendezéssel és a szinusz-tétel felhasználásával (1) így alakítható:

\begin{matrix} \frac{sin α}{sin γ} + \frac{sin β}{sin γ} = cos α + cos β, \frac{a}{c} + \frac{b}{c} = cos α + cos β, \\ a + b = c cos α + c cos β . & (2) \end{matrix}

1. ábra

2. ábra

α

és

β

hegyesszögek, akkor a jobb oldal tagjai az

A B_{1}

B A_{1}

szakaszok hosszát adják, ahol

A_{1}

B_{1}

magasságtalppontok (1. ábra). Mármost ha

γ

hegyesszög, akkor

A B_{1} < A C = b

B A_{1} < B C = a

, tehát

c cos α + c cos β < a + b

, ellentétben a feltevés (2) alakjával. Ha pedig

γ

tompaszög, akkor

A B_{1} > A C

B A_{1} > B C

, és így

c cos α + c cos β > a + b

(2. ábra).
Ha

α

és

β

egyike, pl.

α

nem hegyes szög:

α \geq 90^{\circ}

, akkor

γ

hegyes szög, és ismét az előbbi első esetre jutunk, ugyanis ekkor is fennáll

c cos α 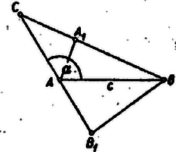\leq 0 < b

(3. ábra).

3. ábra

Könnyű belátni viszont, hogy,

γ = 90^{\circ}

esetén (1) teljesül, így ugyanis

cos α = sin β

cos β = sin α

és mindkét oldalon 1 áll.

Lippai Pál (Szeged, Radnóti M. g. IV. o. t.)

Megjegyzések. 1. A (2) összefüggést (1)-nek

a b c

-vel való szorzásával, majd a terület 2-szeresével való osztásával is megkaphatjuk:

\begin{matrix} \frac{a (b c sin α) + b (a c sin β)}{cos α + cos β} = c (a b sin γ), \frac{a + b}{cos α + cos β} = c . \end{matrix}

Parragh Zoltán (Budapest, I. István g. III. o. t.)

2. Számos dolgozat az állítás fordítottját bizonyította, vagyis hogy derékszögű háromszögben fennáll (1). Ezek a kitűzött feladatot nem oldották meg.