Kezdőlap


Feladat:	1138. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nóber Ilona
Füzet:	1962/október, 67 - 69. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Alakzatok hasonlósága, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1961/november: 1138. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a három körív (szerkesztésük sorrendjében) $k_{1}$ , $k_{2}$ , $k_{3}$ , a $k_{1}$ középpontja $O$ , a metsző $e$ egyenesnek $B C$ -vel bezárt szöge $B C D ∢ = φ$ , végül $B$ -nek vetülete $e$ -re $K$ , és $e$ -re vonatkozó tükörképe $L$ . $k_{1}$ -et egész körré kiegészítve átmegy $C$ -n. $L$ a $k_{3}$ -on, vagy meghosszabbításán, a $C$ körül $C A$ sugárral írt kör kerületén van. ‐ Megmutatjuk, hogy a kérdéses idomok mindegyike egyenlő területű a $B K D$ háromszöggel.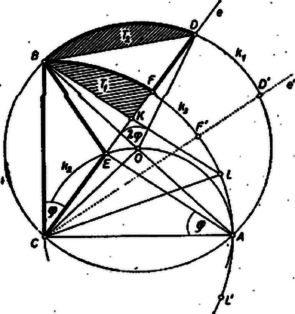
A kerületi szögek tétele szerint $k_{1}$ -ben $B D C ∢ = B A C ∢ = 45^{\circ}$ , ezért a $B D K$ derékszögű háromszög egyenlő szárú: $K D = B K$ . Másrészt a $C B K$ és $A C E$ derékszögű háromszögek egybevágók ‐ mert $k_{2}$ az $A C$ átmérő fölötti Thalész-kör, így $E A C$ és $K C B$ merőleges szárú hegyesszögek, és $A C = B C$ ‐, ezért $C E = B K = K D$ . Így az egyenlő alapú és közös magasságú $B K D$ és $B C E$ háromszögek területe valóban egyenlő.

D F

szakasz és a

B D

B F

ívek határolta

T

idomból úgy nyerhetjük a

B D K

háromszöget, hogy kiegészítjük a

B K

K F

szakaszok és a

B F

is határolta

T_{1}

idommal a

B K

és

K D

szakaszok és a

B D

ív határolta idommá, majd ebből elhagyjuk a

B D

húr és a

B D

ív közti (kisebb)

T_{2}

körszeletet. Elegendő tehát még azt megmutatnunk, hogy

T_{1}

és

T_{2}

területe egyenlő. A

T_{2}

-höz tartozó

B O D

középponti szög egyenlő a

B C D = φ

szög 2-szeresével, és így egyenlő a

B C L

szöggel. A

T_{1}

viszont az utóbbi szöghöz mint középponti szöghöz

k_{3}

-ban tartozó

B F L = T_{3}

körszelet fele. Ezért a

T_{2}

és

T_{3}

körszeletek hasonlók, így területük aránya egyenlő a megfelelő körsugarak négyzetének

B O^{2} : B C^{2}

arányával. Ennek értéke 1/2, mert a

B O C

derékszögű háromszög egyenlő szárú, ezért

T_{2}

területe fele akkora, mint

T_{3}

-é, tehát egyenlő

T_{1}

területével. Ezt akartuk bizonyítani.

II. megoldás. A fenti jelöléseket ezután is használjuk, továbbá hosszúságegységnek vesszük az

A C = B C

befogót. Így

B C E

területe

\begin{matrix} \frac{1}{2} \cdot C E \cdot B K = \frac{1}{2} A C sin φ \cdot B C sin φ = \frac{1}{2} sin^{2} φ . \end{matrix}

(1)

A másik vizsgálandó idomot úgy kapjuk, hogy a

B D O

körcikkből és a

B O C

háromszögből álló idomból

φ \leq 45^{\circ}

esetén elvesszük ‐ ha pedig

45^{\circ} < φ \leq 90^{\circ}

, akkor hozzá tesszük ‐ a

D O C

háromszöget, végül a nyert idomból elvesszük a

B F C

körcikket. Jelöljük a

B D O

körcikk, a

B O C

háromszög, a

D O C

háromszög és a

B F C

körcikk területét rendre

t_{1}

t_{2}

t_{3}

t_{4}

-gyel.
A körcikkek sugarának négyzete

D O^{2} = 1 / 2

, ill.

B C^{2} = 1

, középponti szögük

2 φ

, ill.

φ

, így

\begin{matrix} t_{1} = \frac{\frac{1}{2} π \cdot 2 φ}{360^{\circ}} = \frac{π φ}{360^{\circ}}, t_{4} = \frac{π φ}{360^{\circ}} . \end{matrix}

Másrészt

t_{2} = 1 / 4

. Az

O D C

háromszög egyenlő szárú, az alapján levő szög

D C O ∢ = 45^{\circ} - φ

, ha

φ \leq 45^{\circ}

és

D C O ∢ = φ - 45^{\circ}

, ha

45^{\circ} < φ \leq 90^{\circ}

, így a szárak közti szög

180^{\circ} - 2 (45^{\circ} - φ) = 90^{\circ} + 2 φ

, ill.

180^{\circ} - 2 (φ - 45^{\circ}) = 270^{\circ} - 2 φ

, ennélfogva

\begin{matrix} t_{3} = \frac{1}{2} D O^{2} sin (90^{\circ} + 2 φ) = \frac{1}{4} cos 2 φ, & ha φ \leq 45^{\circ}, és \\ t_{3} = \frac{1}{2} D O^{2} sin (270^{\circ} - 2 φ) = - \frac{1}{4} cos 2 φ, & ha 45^{\circ} < φ \leq 90^{\circ} . \end{matrix}

Mivel a

t_{3}

terület az első esetben levonandóként szerepel, a második esetben hozzáadandóként, azért a keresett idom területére mindkét esetben

\begin{matrix} \frac{π φ}{360^{\circ}} + \frac{1}{4} - \frac{1}{4} cos 2 φ - \frac{π φ}{360^{\circ}} = \frac{1}{4} (1 - cos 2 φ) = \frac{1}{4} \cdot 2 sin^{2} φ = \frac{1}{2} sin^{2} φ \end{matrix}

adódik. Ez egyezik (1)-gyel, így a feladat állítását igazoltuk.

Nóber Ilona (Szentendre, Móricz Zs. g. III. o. t.)