Kezdőlap


Feladat:	1135. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szerdahelyi Károly
Füzet:	1962/október, 64 - 65. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1961/november: 1135. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A vizsgálandó kifejezés így írható

\begin{matrix} K = (y_{1} + y_{4}) - (y_{2} + y_{3}) = (y_{4} - y_{3}) - (y_{2} - y_{1}) = c (x_{4}^{2} - x_{3}^{2}) - \\ - c (x_{2}^{2} - x_{1}^{2}) = c (x_{4} - x_{3}) (x_{4} + x_{3}) - c (x_{2} - x_{1}) (x_{2} + x_{1}) = \\ = c h (2 b + 2 d + h) - c h (2 b - 2 d - h) = c h (4 d + 2 h) = 2 c h (2 d + h) . \end{matrix}

Az utolsó alak valóban nem tartalmazza

b

-t, független tőle.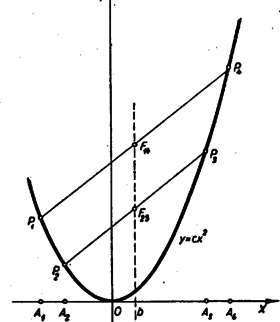

Látható, hogy az

X

-tengely

x_{1}

és

x_{4}

, valamint

x_{2}

és

x_{3}

abszcisszájú

A_{1}

A_{4}

, ill.

A_{2}

A_{3}

pontjai a

b

abszcisszára nézve tükrös párok. Eszerint az

y = c x^{2}

függvény grafikonján a megfelelő

P_{1}

és

P_{4}

, ill.

P_{2}

és

P_{3}

pontok közti húrok

F_{14}

, ill.

F_{23}

felezőpontjai is a

b

abszcisszán vannak, egymás fölött. A

\begin{matrix} \frac{K}{2} = \frac{y_{1} + y_{4}}{2} - \frac{y_{2} + y_{3}}{2} = c h (2 d + h) \end{matrix}

érték éppen a két felezőpont magasságkülönbségét, egyben távolságát adja meg. A két húr párhuzamos, mert

\begin{matrix} \frac{y_{4} - y_{1}}{x_{4} - x_{1}} = c (x_{4} + x_{1}) = 2 b c = \frac{y_{3} - y_{2}}{x_{3} - x_{2}} . \end{matrix}

Eszerint az

A_{1}

A_{2}

A_{3}

A_{4}

pontrendszert mint merev egységet az

X

-tengely mentén eltolva a megfelelő

P_{1} P_{4}

és

P_{2} P_{3}

húrok meredeksége változik, de felezőpontjaik távolsága állandó.
Más átalakítással

\begin{matrix} \frac{K}{h} = \frac{y_{4} - y_{3}}{h} - \frac{y_{2} - y_{1}}{h} = \frac{y_{4} - y_{3}}{x_{4} - x_{3}} - \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = 2 c (2 d + h) = \\ = 2 c (x_{3} - x_{1}) = 2 c (x_{4} - x_{2}) . \end{matrix}

Innen azt olvashatjuk ki, hogy az

A_{1}

A_{2}

merev pontpárt

A_{3}

A_{4}

-be tolva a

P_{1} P_{2}

húr meredekségének változása arányos az

x_{3} - x_{1}

eltolással. Ugyanezt adja természetesen a

\begin{matrix} \frac{K}{2 d + h} = \frac{y_{4} - y_{2}}{x_{4} - x_{2}} - \frac{y_{3} - y_{1}}{x_{3} - x_{1}} = 2 c h = 2 c (x_{2} - x_{1}) \end{matrix}

alakítás is az

A_{1}

A_{3}

pontpárnak

A_{2}

A_{4}

-be való eltolására.

d = 0

esetén

x_{2} = x_{3} = b = (x_{1} + x_{4}) / 2

y_{2} = y_{3}

, és

\begin{matrix} \frac{K}{2} = \frac{y_{1} + y_{4}}{2} - y_{2} = c h^{2} . \end{matrix}

Eszerint, ha az

A_{1} A_{4}

szakasz felezőpontja

A_{2}

, akkor a

P_{1} P_{4}

húr felezőpontjának

P_{2}

-től való távolsága az

A_{1}

A_{2}

A_{4}

merev pontrendszer eltolásával nem változik. A távolság arányos az

A_{1} A_{2}

szakasz négyzetével.
Másképpen, mindegyik

y

ordinátát kifejezve a megfelelő abszcisszával, majd

c

-vel osztva

\begin{matrix} (\frac{K}{2 c} =) \frac{x_{1}^{2} + x_{4}^{2}}{2} - x_{2}^{2} = h^{2}, \frac{x_{1}^{2} + x_{4}^{2}}{2} = {(\frac{x_{1} + x_{4}}{2})}^{2} + {(\frac{x_{4} + x_{1}}{2})}^{2} \end{matrix}

azaz két szám négyzetének számtani közepe az alapok közepének négyzeténél annyival nagyobb, mint a különbségük felének a négyzete.

Szerdahelyi Károly (Budapest, élelmiszerip. t. III. o. t.)