Kezdőlap


Feladat:	1132. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hegedűs Barna , Vida György
Füzet:	1962/szeptember, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Terület, felszín, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1961/október: 1132. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C$ háromszög oldala $a$ . Abban a speciális esetben, ha $P$ pl. az $A$ csúcsba esik, $P A^{2} + P B^{2} + P C^{2} = 0 + a^{2} + a^{2} = 2 a^{2}$ , azt kell tehát megmutatnunk, hogy a kérdéses négyzetösszeg értéke $P$ minden helyzetében $2 a^{2}$ . A szimmetria miatt elég pl. a rövidebb $B C$ íven fekvő $P$ pontokat tekintenünk. Így 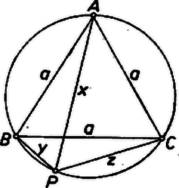$A P B ∢ = A P C ∢ = 60^{\circ}$ , és $B P C ∢ = 120^{\circ}$ .

Ha egy

D E F

háromszögben

D E F ∢ = 60^{\circ}

, és az oldalak hossza

E F = d

F D = e

D E = f

, ahol

d \geq f

, és

D

-nek

E F

-en levő vetülete

D'

, akkor ismeretes, hogy a

D E D'

derékszögű háromszögben

E D' = f / 2

D D' = f \sqrt[]{3} / 2

, és így a

D F D'

derékszögű háromszögből

\begin{matrix} e^{2} = \frac{3 f^{2}}{4} + {(d - \frac{f}{2})}^{2} = d^{2} + f^{2} - d f . \end{matrix}

Hasonlóan, ha

D E F ∢ = 120^{\circ}

, akkor

\begin{matrix} e^{2} = \frac{3 f^{2}}{4} + {(d + \frac{f}{2})}^{2} = d^{2} + f^{2} + d f . \end{matrix}

A háromszög területe pedig mindkét esetben

\begin{matrix} t = \frac{d f \sqrt[]{3}}{4} . \end{matrix}

Alkalmazzuk ezeket az

A P B

A P C

B P C

háromszögre. Legyen

P A = x

P B = y

P C = z

, így

\begin{matrix} A B^{2} = a^{2} = x^{2} + y^{2} - x y, A C^{2} = a^{2} = x^{2} + z^{2} - x z, \\ B C^{2} = a^{2} = y^{2} + z^{2} + y z, \end{matrix}

amiből összeadással

\begin{matrix} 3 a^{2} = 2 (x^{2} + y^{2} + z^{2}) - (x y + x z - y z) . \end{matrix}

(1)

Másrészt az első két háromszög területének összegéből a harmadik háromszög területét kivonva az

A B C

háromszög területét kapjuk:

\begin{matrix} \frac{x y \sqrt[]{3}}{4} + \frac{x z \sqrt[]{3}}{4} - \frac{y z \sqrt[]{3}}{4} = \frac{a^{2} \sqrt[]{3}}{4}, \end{matrix}

amiből egyszerűsítéssel

\begin{matrix} x y + x z - y z = a^{2} . \end{matrix}

Ezt (1)-be helyettesítve átrendezés és osztás után

\begin{matrix} x^{2} + y^{2} + z^{2} = 2 a^{2}, \end{matrix}

amit bizonyítani akartunk.

Hegedűs Barna (Debrecen, Tóth Á. g. III. o. t.)

II. megoldás. Megmutatjuk, hogy a kérdéses négyzetösszeg minden olyan esetben állandó, ha

P

egy az

A B C

háromszög köré írt

k

körrel koncentrikus

k_{1}

körön fut végig. Legyen

k

középpontja

O

, sugara

r

és

O P = R

, állandó, továbbá jellemezzük

P

helyzetét az

A O P = φ

szöggel. A szimmetria miatt elegendő pl. az

A O B

szögtér egyik felében levő

P

pontokat vizsgálni, tehát pl. a

0^{\circ} \leq φ \leq 60^{\circ}

értékekre szorítkozni.

P O A

P O B

P O C

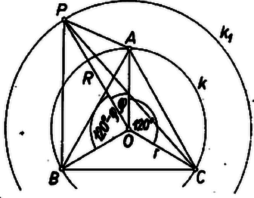háromszögből a koszinusz‐tétel alapján

\begin{matrix} P A^{2} & = r^{2} + R^{2} - 2 r R cos φ, \\ P B^{2} & = r^{2} + R^{2} - 2 r R cos (120^{\circ} - φ), \\ P C^{2} & = r^{2} + R^{2} - 2 r R cos (120^{\circ} + φ) . \end{matrix}

φ = 0^{\circ}

esetén a

P O A

φ = 60^{\circ}

esetén a

P O C

háromszög elfajul, de az egyenlőség helyes marad. Összeadással és kiemeléssel

\begin{matrix} P A^{2} + P B^{2} + P C^{2} = 3 r^{2} + 3 R^{2} - 2 r S, ahol \\ S = cos φ + cos (120^{\circ} - φ) + cos (120^{\circ} + φ) . \end{matrix}

Megmutatjuk, hogy

S

értéke 0. A koszinuszfüggvény összegezési tétele szerint a 2-ik és 3-ik tagban a

sin 120^{\circ} sin φ

sorozat ellentett előjellel lép fel, kiesik. Így,

cos 120^{\circ} = - 1 / 2

figyelembevételével

\begin{matrix} S = cos φ + 2 cos 120^{\circ} cos φ = cos φ - cos φ = 0. \end{matrix}

Ezzel állításunkat bebizonyítottuk, a négyzetösszeg

3 r^{2} + 3 R^{2}

értéke valóban független

φ

-től,

P

-nek a

k_{1}

körön elfoglalt helyzetétől.
Ha

k_{1}

azonos

k

-val, akkor

\begin{matrix} P A^{2} + P B^{2} + P C^{2} = 6 r^{2}, \end{matrix}

és mivel

a / r = \sqrt[]{3}

, azért eredményünk megegyezik az I. megoldás eredményével.

Vida György (Budapest, Madách I. g. IV. o. t.)