Feladat: 1131. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Aleva György 
Füzet: 1962/szeptember, 22 - 24. oldal  PDF  |  MathML 
Témakör(ök): Súlypont, Mértani helyek, Térelemek és részeik, Feladat
Hivatkozás(ok):Feladatok: 1961/október: 1131. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük először az L pont mértani helyét, ha A' befutja az ε síkot. Legyen A vetülete ε-ra A1, és az AA1 szakasz hossza a(≠0). Ha A' egybeesik A1-gyel, akkor L az AA1 szakasz A0 felezőpontjában van. A' minden más helyzetében az LA0 egyenes felezi az AA1A' háromszög AA1 és AA' oldalait, tehát e háromszögnek középvonala. Ezért LA0 párhuzamos A1A'-vel, tehát ε-nal is. Így L mindig benne van az A0-on átmenő, ε-nal párhuzamos α síkban. Ez a sík egyszersmind L mértani helye is, mert ha α-nak egy tetszés szerinti pontja L, akkor az AL egyenes metszi ε-t egy A' pontban, és az AA' szakasz felezőpontja 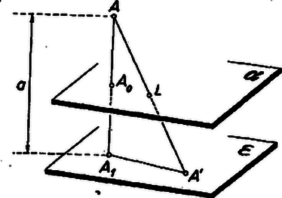L.

 
 
1. ábra
 

Hasonlóan M és N mértani helye az az ε-nal párhuzamos β, ill. γ sík, amely ε-nak azon az oldalán van, mint A, B és C, és ε-tól való távolsága b/2, ill. c/2, ahol b a B-nek, c a C-nek ε-tól mért távolsága.
Legyen most A', B', C' az ε sík olyan ponthármasa, hogy a képezett L, M N pontok háromszöget alkotnak. G-t megadja az LM szakasz N0 felezőpontját N-nel összekötő szakasznak N0-tól számított első harmadoló pontja, vagyis amelyre N0G=N0N/3. Feltehetjük, hogy A, B, C-nek ε-tól mért távolságaira fennáll a≤b≤c (egyenlőség csak az egyik helyen állhat, különben az ABC sík párhuzamos lenne ε-nal). Ekkor a β sík (b-a)/2-vel távolabb fekszik ε-tól, mint az a sík. A fentiekhez hasonlóan adódik, hogy N0 rajta fekszik azon az ε-nal párhuzamos ν síkon, amely ε-nak azon az oldalán van, mint A, B, C és ε-tól mért távolsága
a2+12(b-a2)=a+b4.
(Ezt először rögzített A' mellett kapjuk ‐ vagyis rögzített L mellett ‐, majd belátjuk, hogy tetszés szerinti A'-vel ugyanerre a mértani helyre jutunk.)
Rögzített A' és B' mellett (azaz állandó L, M és N0 mellett) hasonlóan adódik, hogy G azon az ε-nal párhuzamos σ síkon fekszik, amely ε-nak A, B, C-vel egyező oldalán van és ε-tól mért távolsága
a+b4+13(c2-a+b4)=16(a+b+c).
Nyilvánvaló ugyanis, hogy G-nek ε-tól mért távolsága annyival több N0-nak ε-tól mért távolságánál, mint a ν és γ síkok távolságának 1/3 része. Ugyanezt kapjuk bármely A'-vel és B'-vel.
Megmutatjuk, hogy a σ sík bármely G pontjához lehet megadni ε-ban olyan A', B', C' ponthármast, amelyekből képezett L, M, N pontok nincsenek egy egyenesen, és az LMN háromszög súlypontja éppen G. Ez az előzőkkel együtt azt jelenti, hogy G mértani helye a 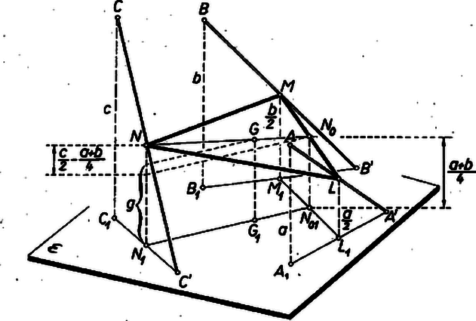σ sík.
 
 
2. ábra
 

Legyen B, C, G vetülete ε-ra B1, C1, G1. Vegyünk ε-ban egy G1 től különböző tetszés szerinti N1 pontot, mérjük fel az N1G1 szakasz G1-en túli meghosszabbítására e szakasz felét, legyen a végpont N01, és mérjünk fel egy az N01-en átmenő, N01G1-től különböző tetszés szerinti egyenesre N01-től mindkét irányban egy tetszés szerinti szakaszt, legyenek a végpontok L1 és M1. Végül vegyük A', B', C' gyanánt A1-nek L1-re, ill. B1-nek M1-re, ill. C1-nek N1-re vett tükörképét. ‐ Ekkor az A', B', C'-ből képezett L, M, N pontok ε-ra való vetülete nyilván L1, M1, N1, továbbá az LMN háromszög G súlypontjának ε-ra való vetülete G1. Ugyanis ‐ párhuzamos vetítés mellett ‐ az egy egyenesen levő szakaszok aránya nem változik meg, egy szakasz felező (ill. harmadoló) pontjának vetülete felezi (harmadolja) a szakasz vetületét. L1, M1, N1 szerkesztésnél fogva háromszöget alkotnak, ezért N nincs benne az ε-ra L1M1-en át merőlegesen álló, az L és M-et magában foglaló síkban, tehát L, M, N is háromszöget alkotnak. ‐ Ezzel az állítás bizonyítását befejeztük.
 
Aleva György (Budapest, Radnóti M. gyak. g. IV. o. t.)