Kezdőlap


Feladat:	1128. matematika feladat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Magyar Erzsébet , Romhányi Gábor , Sonnevend György
Füzet:	1962/május, 209 - 211. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1961/október: 1128. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A bizonyítandó egyenlőtlenség bal oldala pozitív és jobb oldala nem negatív. Ezért mindkét oldalát négyzetre emelve az

\begin{matrix} {(a^{2} + b^{2} + c^{2})}^{2} = (a^{4} + b^{4} + c^{4}) + 2 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) \geq 48 S^{2} \end{matrix}

(2)

egyenlőtlenség vele ekvivalens, elegendő ezt bizonyítanunk.
A Heron-képlet mindkét oldalát négyzetre emelve beszorzás és a törtek eltávolítása után (2) jobb oldalának

3

-ad részét kapjuk:

\begin{matrix} 16 S^{2} = - (a^{4} + b^{4} + c^{4}) + 2 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) . \end{matrix}

Ezt felhasználva (2) bal és jobb oldalának különbsége így alakítható:

\begin{matrix} 4 (a^{4} + b^{4} + c^{4}) + 4 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) = \\ = 2 [{(a^{2} - b^{2})}^{2} + {(b^{2} - c^{2})}^{2} + {(c^{2} - a^{2})}^{2}] . & (3) \end{matrix}

Ez nyilván sohasem negatív, tehát (2) és vele (1) minden háromszögre érvényes. Egyenlőség (2)-ben és (1)-ben akkor és csak akkor áll fenn, ha (3) jobb oldalán mind a három különbség

0

-val egyenlő. Az

a^{2} - b^{2} = (a - b) (a + b) = 0

követelményből

a - b = 0

a = b

, hiszen

a + b > 0

. A másodikból ugyanígy

b = c

. Ezek szerint

a = b = c

, így pedig (3) harmadik különbsége is

0

. Tehát (1) két oldala akkor és csak akkor egyenlő, ha a háromszög szabályos.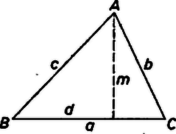

Magyar Erzsébet (Ócsa, Bolyai J. g. IV. o. t.)

II. megoldás. Legyen adva egy háromszög. Jelöljük a csúcsait

A

B

C

-vel úgy, hogy a

B

csúcsnál hegyesszög legyen. Az

A

csúcsból húzott magasság legyen

m

, talppontjának távolsága

B

-től

d

1. ábra

Ekkor

\begin{matrix} a^{2} + b^{2} + c^{2} - 4 \sqrt[]{3} S & = a^{2} + [m^{2} + {(a - d)}^{2}] + (m^{2} + d^{2}) - 2 \sqrt[]{3} a m = \\ = 2 a^{2} - 2 a d + 2 d^{2} - 2 \sqrt[]{3} a m + 2 m^{2} = \\ = \frac{1}{2} (a^{2} - 4 a d + 4 d^{2} + 3 a^{2} - 4 \sqrt[]{3} a m + 4 m^{2}) & = \\ = \frac{1}{2} [{(a - 2 d)}^{2} + {(\sqrt[]{3} a - 2 m t)}^{2}] . \end{matrix}

Ez a kifejezés nem lehet negatív, s így

\begin{matrix} a^{2} + b^{2} + c^{2} \geq 4 \sqrt[]{3} S . \end{matrix}

Továbbá

0

is csak akkor lehet a fent nyert kifejezés, ha

d = a / 2

, tehát a háromszög egyenlőszárú

(b = c)

, továbbá

m = \sqrt[]{3} a / 2

, ami az egyenlő szárú háromszögek közül a szabályosnál következik be. Az éppen bebizonyított egyenlőtlenségben az egyenlőség tehát csak a szabályos háromszögekre áll fenn.

III. megoldás. Tekintsük állandónak az

a^{2} + b^{2} + c^{2}

négyzetösszeget és keressük meg,

a

b

c

mely értékrendszere mellett maximális a háromszög területe, és mennyi ez a maximum.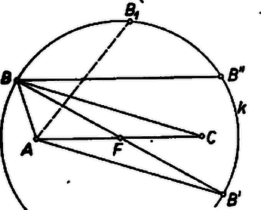

2. ábra

Tegyük fel, hogy

a

b

c

nem mind egyenlők. Ekkor van köztük

\begin{matrix} d = \sqrt[]{\frac{a^{2} + b^{2} + c^{2}}{3}} \end{matrix}

-nál nagyobb is, kisebb is, legyen ez

a

, ill.

c

. A csúcsokat a szokás szerint jelölve tükrözzük a háromszöget az

A C = b

oldal

F

felezőpontjára. A nyert

A B C B'

paralelogrammában az oldalak négyzetösszege ismert tétel szerint¹ egyenlő az átlók négyzetösszegével:

\begin{matrix} 2 (a^{2} + c^{2}) = b^{2} + 4 s^{2}, \end{matrix}

(4)

ahol

s = B F

, a háromszög

A C

oldalához tartozó súlyvonal. Ez azt jelenti, hogy ha

A

-t és

C

-t rögzítjük, akkor

B

mértani helye egy az

F

középpont körüli

k

kör, mert így

b

, vele

a^{2} + c^{2}

, és (4) szerint

s

is állandó.
Távolítsuk

B

-t

A

-tól a

k

-n addig a

B_{1}

helyzetig, amelyre

A B_{1} = d

. Ilyen helyzet van, mert a távolság folytonosan növekszik, és van

k

-n az

A

-tól

d

-nél távolabbi pont, ilyen

B

-nek az

A C

felező merőlegesére való

B''

tükörképe, amelyre

A B'' = C B = a > d

. Ebből azt is látjuk, hogy

B_{1}

B B''

íven van, tehát az

A C B_{1}

háromszög területe nagyobb

A B C

területénél, mert az előbbiben a közös

A C

alaphoz tartozó magasság nagyobb.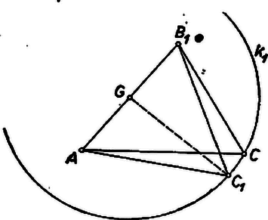

3. ábra

Most már az

A B_{1} = c = d

oldalt rögzítve

C

mértani helye egy az

A B_{1}

-nek

G

felezőpontja körüli

k_{1}

kör, és a terület nyilván arra a

C_{1}

-re maximális, amelyre

C_{1} G ⊥ A B_{1}

, vagyis

a = b

, és így a háromszög szabályos,mert

\begin{matrix} a^{2} = b^{2} = \frac{3 d^{2} - c^{2}}{2} = c^{2} . \end{matrix}

Ekkor a terület

S = a^{2} \sqrt[]{3} / 4

, és

4 \sqrt[]{3} S = 3 a^{2} = a^{2} + b^{2} + c^{2}

, tehát (1)-ben egyenlőség áll. Minden más esetben

S

-sel együtt (1) jobb oldala kisebb. Ezzel az állítást bebizonyítottuk.
Kóta Józsefnek az Olimpián írt dolgozatából.

Megjegyzések. I. Az állítást annak az ismert eredménynek² a felhasználásával is bizonyíthatjuk, hogy ugyanakkora kerületű háromszögek közül a szabályos háromszög területe a legnagyobb. Nyilvánvalóan elegendő ugyanis azokat a háromszögeket vizsgálnunk, amelyekben

a + b + c = 2 s

, állandó. Szabályos háromszög esetében

a = b = c = 2 s / 3 = a'

, ekkor (1) két oldala egyenlő, közös értékük

4 s^{2} / 3

. Megmutatjuk, hogy minden más esetben (1) bal oldala nagyobb ennél. Legyen az első két oldal értéke

a = a' + x

b = a' + y

, ahol

x

és

y

közül legalább az egyik

0

-tól különböző. Így a harmadik oldal:

c = 2 s - 2 a' - x - y = a' - (x + y)

, és a négyzetösszeg:

\begin{matrix} {(a' + x)}^{2} + {(a' + y)}^{2} + {[a' - (x + y)]}^{2} = 3 a'^{2} + x^{2} + y^{2} + {(x + y)}^{2} > 3 a'^{2} = \frac{4 s^{2}}{3} . \end{matrix}

A jobb oldal viszont a hivatkozott eredmény szerint kisebb, tehát minden más esetben (1)-ben valóban a

>

jel érvényes.

Romhányi Gábor (Esztergom, Temesvári P. g. IV. o. t.)

2. Az állításnak az

a_{1}, a_{2}, ..., a_{n}

oldalakkal bíró

S_{n}

területű

n

-szögre

(n > 3)

való

\begin{matrix} a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2} \geq 4 S_{n} tg\frac{π}{n} \end{matrix}

általánosítása az I. megjegyzés gondolatmenetéhez hasonlóan bizonyítható.

Sonnevend György (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

¹Lásd pl. 1006. feladat, K. M. L. 21 (1960/9) 20. o.

²Lásd $n$ -szögre $(n \geq 3)$ Hódi Endre: Szélsőérték-feladatok elemi megoldása (Tankönyvkiadó, Budapest, 1959) 48. o.