Kezdőlap


Feladat:	1125. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Benczúr András , Csákó Gy. , Jójárt I. , Kunszt Z. , Lehel J. , Orbán Szilvia , Reuss P. , Vág I. , Zalán P.
Füzet:	1962/május, 205 - 207. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Hossz, kerület, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1125. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Legyen az $O$ középpont körüli $r$ sugarú körbe írt szabályos $n$ -szög egy oldala $C D = a_{n}$ , a rövidebb $C D$ ív felezőpontja $E$ , így a beírt szabályos $2 n$ -szög oldala $C E = a_{2 n}$ . Húzzuk meg továbbá a kör érintőjét $C$ , $D$ és $E$ -ben, legyen az első két érintő metszéspontja $F$ , és messe a harmadik az első kettőt $G$ , $H$ -ban. Így $C F$ és $D F$ fele akkora, mint a körülírt szabályos $n$ -szög $A_{n}$ oldala, $G H$ pedig a körülírt szabályos $2 n$ -szög $A_{2 n}$ o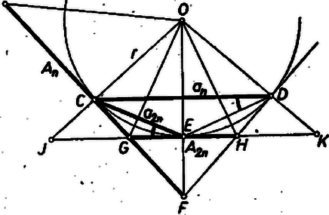ldala.

E jelölésekkel

K_{n} = n A_{n}

k_{n} = n a_{n}

K_{2 n} = 2 n A_{2 n}

k_{2 n} = 2 n a_{2 n}

, és a bizonyítandó összefüggések így alakulnak:

\begin{matrix} A_{2 n} = \frac{A_{n} a_{n}}{A_{n} + a_{n}}, & (2) \\ a_{2 n} = \sqrt[]{\frac{a_{n} A_{2 n}}{2}} . & (3) \end{matrix}

G

-ből húzott érintők egyenlősége alapján

G C = G E = A_{2 n} / 2

, ezért

F G = F C - G C = A_{n} / 2 - A_{2 n} / 2 = (A_{n} - A_{2 n}) / 2

G H

párhuzamos

C D

-vel, így a

C D F

és

G H F

háromszögek hasonlóságából:

\begin{matrix} C D : G H = C F : G F, azaz a_{n} : A_{2 n} = \frac{A_{n}}{2} : \frac{A_{n} - A_{2 n}}{2}, \end{matrix}

és ebből

A_{2 n}

-t kifejezve (2)-re jutunk.
A

C D E

és

C E G

egyenlő szárú háromszögek ugyancsak hasonlók, mert az alapon fekvő

D C E

, ill.

C E G

szögek váltószögek. Így

\begin{matrix} C D : C E = C E : C G, azaz a_{n} : a_{2 n} = a_{2 n} : \frac{A_{2 n}}{2}, \end{matrix}

ez pedig (3)-ra vezet. Ezzel az állítást bebizonyítottuk.
2. Ismeretes, hogy

K_{4} = 8 r

és

k_{4} = 4 \sqrt[]{2} r \approx 5,6569 r

. Ezekből az (1) képletekkel

\begin{matrix} K_{8} = \frac{2 K_{4} k_{4}}{K_{4} + k_{4}} = 16 (\sqrt[]{2} - 1) r \approx 6, 6274 r, \\ k_{8} = \sqrt[]{k_{4} K_{8}} = 8 \sqrt[]{2 - \sqrt[]{2}} r \approx 6, 1229 r . \end{matrix}

Másrészt

K_{6} = 4 \sqrt[]{3} r \approx 6, 9282 r

és

k_{6} = 6 r

, és így

\begin{matrix} K_{12} = \frac{2 K_{6} k_{6}}{K_{6} + k_{6}} = 24 (2 - \sqrt[]{3}) r \approx 6, 4308 r, \\ k_{12} = \sqrt[]{k_{6} K_{12}} = 12 \sqrt[]{2 - \sqrt[]{3}} r = 6 (\sqrt[]{6} - \sqrt[]{2}) r \approx 6, 2117 r; \\ K_{24} = \frac{2 K_{12} k_{12}}{K_{12} + k_{12}} = 48 (\sqrt[]{3} - \sqrt[]{2}) (\sqrt[]{2} - 1) r \approx 6, 3193 r . \\ k_{24} = \sqrt[]{k_{12} K_{24}} = 12 \sqrt[]{8 - 2 \sqrt[]{6} - 2 \sqrt[]{2}} r \approx 6, 2653 r . \end{matrix}

Orbán Szilvia (Budapest, Kaffka M. lg. IV. o. t.)

Megjegyzések. 1: A (2) összefüggést másképpen is megkaphatjuk. Messe pl.

O C

O D

E

-beli érintőt

J

, ill.

K

-ban, így

J K = A_{n}

. Mivel

O G

felezi a

J O E

szöget, azért a szögfelező osztásarányára ismert tétel szerint

\begin{matrix} E G : G J = O E : O J = O C : O J = C D : J K, azaz \\ \frac{A_{2 n}}{2} : \frac{A_{n} - A_{2 n}}{2} = a_{n} : A_{n} . \end{matrix}

Benczur András (Budapest, Fazekas M. gyak. g. IV. o. t.)

2. A dolgozatok legnagyobb része trigonometriai képletek és goniometriai azonosságok felhasználásával bizonyította az állításokat; vagyis a fentieknél erősebb eszközökkel, és minden esetben hosszabb úton. Erre nem volt szükség.
3. Bár a bizonyítást a (2) és (3) alakban a sokszögek oldalaira végeztük, az állítást ‐ történeti okból ‐ mégis a kerületekre mondtuk ki. Ugyanis Archimedész a fenti képletpárral számította a

6

12

24

48

és

96

oldalú körülírt és beírt sokszögek kerületét és a

\begin{matrix} K_{6}, k_{6}, K_{12}, k_{12}, K_{24}, k_{24}, K_{48}, k_{48}, K_{96}, k_{96} \end{matrix}

sorozatból egyre kisebb eltérésű egyenlőtlenségpárokat kapott a kör

k

kerületének két határ közé zárásához:

k_{6} < k < K_{6}

k_{12} < k < K_{12}

, s. í. t. Ezt az eljárást nevezi a matematika története archimedészi algoritmusnak (lépésről lépésre való műveletsorozatnak).
4. (2) és (3) természetesen akkor is érvényesek, ha

a_{n}

a kör egy tetszés szerinti húrja,

A_{n}

a vele párhuzamos, közelebbi érintőből a húr végpontjaihoz tartozó sugarakkal kimetszett szakasz,

a_{2 n}

a húrral lemetszett rövidebb ív feléhez tartozó húr, végül

A_{2 n}

ugyanúgy áll elő

a_{2 n}

-ből, mint

A_{n}

a_{n}

-ből.