Kezdőlap


Feladat:	1123. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antal Kálmán , Kéry Gerzson , Kunszt Zoltán
Füzet:	1962/május, 201 - 204. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Húrnégyszögek, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1123. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A keresett $A B C$ háromszögben az adott $A C B$ szög $C D = f$ felezője meghosszabbításának a $k$ körülírt körrel való $E$ metszéspontja felezi a $C$ -t nem tartalmazó $A B$ ívet, mert az $A C E$ és $E C B$ kerületi szögek egyenlők. Másrészt a $B E$ íven fekvő $E A B$ és $E C B$ szögek is egyenlők. Így az $A D E$ és $C A E$ háromszögek hasonlók, mert $E$ -nél levő szögük közös, tehát

\begin{matrix} A E : E D = C E : E A . \end{matrix}

Itt

A E

ismert szakasz, mert az

A B = c

oldalból és az

A C B

szögből

k

, továbbá rajta

E

megszerkeszthető. Ennélfogva az adódó

\begin{matrix} E D \cdot E C = E D (E D + D C) = E D (E D + f) = E A^{2} \end{matrix}

(1)

egyenlőség felhasználásával

E D

és

E C

is szerkeszthetők, pl. a körhöz külső pontból húzott szelőn és érintőn létrejött szakaszokra ismert tétel alapján, ha a szelőnek a körbe eső húrját

f

-nek, az érintő hosszát pedig

A E

-nek vesszük.

1. ábra

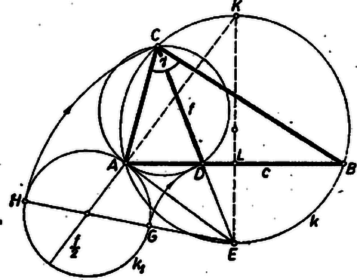A segédszerkesztés célszerűen úgy végezhető, hogy az

A E

-t

A

-ban érintő,

f

átmérőjű

k_{1}

kört vesszük és meghúzzuk ehhez

E

-ből a középpontján átmenő

E G H

szelőt (ahol

E G < E H

). Ekkor

E G \cdot E H = E A^{2}

. Mivel

G H = f

, így

\begin{matrix} E G = E D; E G + G H = E D + f = E C, \end{matrix}

tehát

C

-t

k

-ból az

E

körül

E H

sugárral írt körívvel metszhetjük ki. (

k_{1}

szerkesztését megkönnyíti az az észrevétel, hogy középpontja az

A K

egyenesen van, ahol

K

k

kör

E

-vel átellenes pontja.)
Az

A B C

háromszög megfelel a feltételnek. Ugyanis

A B

egyenlő az adott szakasszal,

C E

felezi az

A C B

szöget, végül

f

-et

C

-ből

E

felé felmérve ‐ vagy ami ugyanaz,

C E

-re

H G

-t ráforgatva ‐ a

D^{*}

végpont

A B

-n van. Valóban, (1) szerint az

A C D^{*}

háromszög körülírt köre érinti

A E

-t, ezért az

E A D^{*}

(húr-érintő) szögre

\begin{matrix} E A D^{*} ∢ = A C D^{*} ∢ = A C E ∢ = E C B ∢ = E A B ∢ . \end{matrix}

k

és

E

egyértelműen szerkeszthető. Nyilvánvaló, hogy

C

létrejön, ha

E H \leq E K

, másképpen: ha

E D \geq E L

, ahol

L

A B

oldal felezőpontja. Ezekből

f

-re is adhatunk feltételt:

\begin{matrix} f = C D = C E - D E \leq K E - L E = K L, \end{matrix}

(2)

vagyis

f

nem lehet nagyobb annál a távolságnál, amennyire az

A B

szakasz

A C B ∢

nyilású látószög-körívének

A B

-től legtávolabbi pontja van. A különböző megoldások száma nyilvánvalóan

1

vagy

0

.
Szerkesztésünk bármely adott

A C B

szög esetén érvényes, mert sehol nem használtuk ki, hogy esetünkben ez a szög derékszög. Derékszögű háromszög esetére (2) így alakul:

f < c / 2

Kunszt Zoltán (Pápa, Türr I. g. IV. o. t.)

II. megoldás. Az I. megoldás szerinti

k

körből

C

-t a

c

átfogóhoz tartozó

m

magasság ismerete alapján is kimetszhetjük.

m

-re egyenletet abból kaphatunk, hogy az

A C D

és

B C D

részháromszögek együttes területe egyenlő az

A B C

háromszög

t

területével.

D

-ből a befogókra bocsátott merőlegesek hossza a létrejövő egyenlő szárú derékszögű háromszögekből

f / \sqrt[]{2}

, ezért

\begin{matrix} 2 t = c m = \frac{a f}{\sqrt[]{2}} + \frac{b f}{\sqrt[]{2}} = \frac{(a + b) f}{\sqrt[]{2}} . \end{matrix}

Innen Pythagorász tétele és

2 t = a b

alapján

\begin{matrix} a + b = \sqrt[]{(a^{2} + b^{2}) + 2 a b} = \sqrt[]{c^{2} + 2 c m} = \frac{\sqrt[]{2} c m}{f}, \end{matrix}

tehát négyzetre emeléssel és rendezéssel

\begin{matrix} 2 c^{2} m^{2} - 2 c f^{2} m - c^{2} f^{2} = 0. \end{matrix}

Ennek gyökei biztosan valósak, mert a tiszta tag negatív, a négyzetes tag együtthatója pedig pozitív. Ebből azt is látjuk, hogy a két gyök ellentett előjelű. A pozitív gyök:

\begin{matrix} m = \frac{f}{c} (\sqrt[]{\frac{f^{2}}{4} + \frac{c^{2}}{2}} + \frac{f}{2}), \end{matrix}

(3)

az adatok alapján mindig megszerkeszthető.
Háromszöget csak akkor kapunk, ha

m \leq c / 2

, azaz

\begin{matrix} \frac{c}{2} \geq \frac{f}{c} (\sqrt[]{\frac{f^{2}}{4} + \frac{c^{2}}{2}} + \frac{f}{2}), \end{matrix}

\begin{matrix} \frac{c^{2}}{f} - f \geq \sqrt[]{f^{2} + 2 c^{2}}, \end{matrix}

amiből négyzetre emeléssel, majd gyökvonással, és figyelembe véve, hogy

c

f

pozitívok

\begin{matrix} c^{4} \geq 4 c^{2} f^{2}, f \leq c / 2. \end{matrix}

Antal Kálmán (Budapest, Kandó K. hír. ip. t. III. o. t.)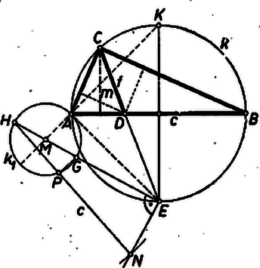

2. ábra

Megjegyzés. (3) szerkesztésében észrevehetjük, hogy a zárójelben álló kéttagú

E M + M H = E H

, ahol

M

k_{1}

kör középpontját jelöli. Eszerint

m = f \cdot E H / c

, tehát

E H

mint befogó fölé

H N = c

átfogóval derékszögű háromszöget szerkesztve

m

-et megadja

H N

-nek a

k_{1}

-be eső

H P

szakasza (2. ábra). (Ez természetesen csak

A C B ∢ = 90^{\circ}

esetén érvényes.)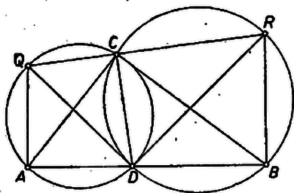

3. ábra

III. megoldás. Megrajzolva az

A C D

és

B C D

háromszög körülírt körét, ezek átmennek azoknak az

A D

-re, ill.

B D

-re mint befogóra szerkesztett

A D Q

, ill.

B D R

egyenlő szárú derékszögű háromszögeknek a

Q

, ill.

R

csúcsán, amelyek

A B

-nek ugyanazon oldalán vannak, mint

C

, és a derékszögek csúcsa

A

, ill.

B

. Így ugyanis

A Q D ∢ = B R D ∢ = 45^{\circ} = A C D ∢ = = B C D ∢

. A létrejött húrnégyszögekből

D C Q ∢ = 180^{\circ} - D A Q ∢ = 90^{\circ} = D C R ∢

, tehát

C

Q R

egyenesen van, és

C D ⊥ Q R

. Másrészt

\begin{matrix} Q D R ∢ = 180^{\circ} - A D Q ∢ - B D R ∢ = 90^{\circ}, \\ és D Q + D R = A D \sqrt[]{2} + B D \sqrt[]{2} = A B \sqrt[]{2} = c \sqrt[]{2} . \end{matrix}

Eszerint a

D Q R

derékszögű háromszögből ismert a befogók összege és az átfogóhoz tartozó

f

magasság. Ha ezt a háromszöget megszerkesztjük, ebből egy az előírásnak megfelelő háromszög csúcsait úgy kapjuk, hogy vesszük az átfogóhoz tartozó magasság talppontját és a befogók fölé kifelé szerkesztett négyzetek középpontját.
A

D Q R

háromszög megszerkesztése a II. megoldáséhoz hasonló számítás alapján történhetik. A befogók összegét

d

-vel, az egyik befogót

a

-val jelölve az átfogó hossza

\sqrt[]{a^{2} + {(d - a)}^{2}}

. A kétszeres terület négyzetét kétféleképpen számítva

\begin{matrix} {[a (d - a)]}^{2} = m^{2} [a^{2} + {(d - a)}^{2}] = m^{2} (d^{2} - 2 a d + 2 a^{2}) = m^{2} d^{2} - 2 m^{2} [a (d - a)] . \end{matrix}

Ez másodfokú egyenlet

a (d - a)

-ra, aminek alapján a befogók mértani közepe, majd az I. megoldás segédszerkesztésének mintájára a befogók megszerkeszthetők. A szerkesztés helyességének bizonyítását és a diszkussziót az olvasóra bizzuk.

Kéry Gerzson (Sopron, Széchenyi I. g. IV. o. t.)