Feladat: 1117. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Kiss Tünde 
Füzet: 1962/április, 161 - 162. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Egyenesek egyenlete, Hiperbola egyenlete, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1961/május: 1117. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az EF egyenes merőleges e és f-re, akkor az EFM háromszög egyenlő szárú, mert így az EM és FM félegyenesek az EF, ill. FE félegyenesből is egyenlő nagyságú és ellentétes irányú forgatással jönnek létre. Kivétel az α=±90∘ eset, mert ekkor e és f egybeesnek, M határozatlan. Nyilvánvaló, hogy ilyenkor a mértani hely az EF szakasz felező merőlegese a felezőpont kivételével.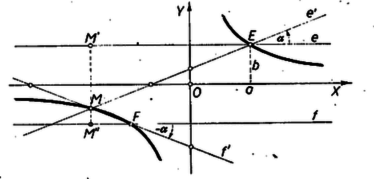

 
 

Ha EF nem merőleges e és f-re, akkor vegyük a szakasz felezőpontját derékszögű koordinátarendszerünk origójának, és legyen az X-tengely párhuzamos e és f-fel. Így E koordinátáit (a,b)-vel jelölve F(-a,-b). Ha még tg α=m, akkor tg (-α)=-m, tehát e', ill. f' egyenlete:
y-b=m(x-a),y+b=-m(x+a).
Így az M metszéspont koordinátái:
x¯=-bm,y¯=-ma.
(m≠0, hiszen α=0∘ és 180∘ esetére nincs metszéspont; számításunk α=±90∘ esetére sem érvényes, de tudjuk, hogy ekkor sincs metszéspont, mert e'∥f'.) m kiküszöbölésével
m=-bx=-y¯a,azazxy¯=ab.
Itt feltevésünknél fogva a≠0; másrészt nyilván b≠0, mert e és f esnek egybe. Eszerint minden M pont rajta van az xy=ab egyenletű egyenlő oldalú hiperbolán, melynek aszimptotái a koordinátatengelyek, és amely átmegy E-n. Látjuk ugyanis, hogy E és F koordinátái is kielégítik az egyenletet (még egyszerűbb azonban, hogy ha e'≡EF, akkor M≡F, ha pedig f'≡EF, akkor M≡E).
Megmutatjuk, hogy e hiperbola minden M pontjára ME és MF egyenlő abszolút értékű, de ellentétes forgási irányú β ill. γ szöget zár be e-vel, ill. f-fel. Ehhez elegendő megmutatnunk, hogy tg β és tg γ összege 0. Valóban y¯=ab/x¯-sal
y¯-bx¯-a+y¯+bx¯+a=abx¯-bx¯-a+abx¯+bx¯+a=b(a-x¯)x¯(x¯-a)+b(a+x¯)x¯(x¯+a)==-bx¯+bx¯=0.


Eszerint a keresett mértani helyet a hiperbola összes pontjai adják.
 
 Kiss Tünde (Tamási, Béri Balogh Á. Gimn. III. o. t.)
 
Megjegyzések. 1. A hiperbola egyenletét e' és f' egyenletének felírása nélkül abból is megkaphatjuk, hogy ha M' és M'' az M vetülete e-n, ill. f-en, akkor az MEM' és MFM'' hasonló derékszögű háromszögek, befogóik aránya egyenlő. Így azonban több eset szétválasztására van szükség aszerint, hogy M az e és f által szétvágott sík melyik félsíkján, ill. a síksávban van. Csak az előjelek vizsgálatával biztosíthatjuk, hogy a koordinátákból helyesen írjuk fel az említett befogók abszolút értékét, másrészt, hogy az M'EM és MFM'' forgások ellentétes irányúak legyenek. Ha pedig ezt elmulasztjuk, akkor a mértani helynek csupán az I. síknegyedbeli részét kapjuk (ha ti. a>0 és b>0).
Ugyanezek a kérdések azoknak a derékszögű háromszögeknek a felhasználásával is fellépnek, amelyeket az e és f-nek a tengelyeken levő metszéspontjaival és M-mel meghatározott egyenlő szárú háromszögekből a magasság meghúzásával kapunk. Az ilyen ,,második megoldások'' többnyire hiányosak.
2. Néhány további, részben elemi megoldás abból vélte kikövetkeztetni, hogy hiperbolával állunk szemben, hogy M és E, ill. M és F egyenlő távol vannak e' ill. f'-nek a tengelyeken levő metszéspontjaitól. Ez az aszimptótás‐tulajdonság minden hiperbolánál fennáll, megvizsgálandó volna azonban, hogy nincs-e más olyan görbe is, amelynek szelőin bizonyos egyenesekre vonatkozóan hasonló egyenlőség áll fenn. Más szóval, hogy ez a tulajdonság a hiperbolának meghatározó tulajdonsága-e.