|
| Feladat: |
1116. matematika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bellay Ágnes , Benczúr András , Bollobás Béla , Farkas Zoltán , Fukker G. , Gagyi Pálffy A. , Gálfi l. , Hegedűs J. , Huber T. , Katona Mária , Kéry G. , Kiss Ildikó , Kóta J. , Kovács Imre , Krámli András , Kunszt Z. , Lehel Cs. , Lehel J. , Máté A. , Máté Eörs , Molnár Emil , Nagypál B. , Náray-Szabó G. , Németh I. , Nováky Béla , Opálény M. , Pór A. , Sebestyén Z. , Simonovits Miklós , Sonnevend Gy. , Strobl Ilona , Szegő K. , Székely Jenő , Szepesvári I. , Szidarovszky Ágnes , Szidarovszky F. , Vesztergombi György , Zalán P. |
| Füzet: |
1962/április,
159 - 160. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Háromszögek hasonlósága, Körök, Háromszögek szerkesztése, Feladat |
| Hivatkozás(ok): | Feladatok: 1961/május: 1116. matematika feladat |
|
|
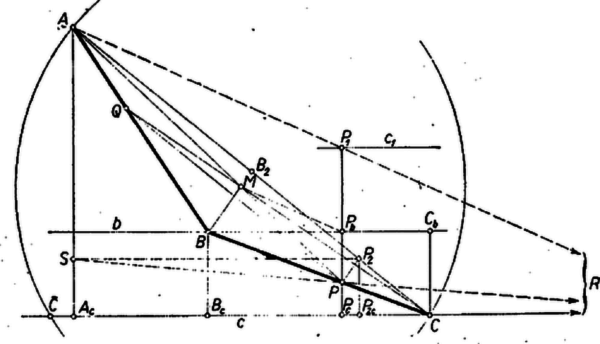
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. A követelményeknek megfelelő útvonal esetén az háromszög egyenlő szárú. Messe -t a -n átmenő, -vel párhuzamos egyenes -ban, legyen az trapéz átlóinak metszéspontja , továbbá és vetülete -n , ill. . Ekkor az , , a , és a , nyilvánvalóan hasonló háromszög‐párokból
Itt az utolsó arány ismert (mert a és egyenesek távolsága), ezért a szakaszon megszerkeszthető(pl. a háromszög felhasználásával, ahol a vetülete -nek -re vett tükörképén, így ‐, -et a -n átmenő -gyel párhuzamos egyenes metszi ki -ból). ismeretében -t -ből az körül írt sugarú körrel metszhetjük ki ─ mivel háromszög egyenlő szárú, s így az trapéz szimmetrikus, tehát ‐, -t pedig a egyenes -vel való metszéspontja adja.
Megmutatjuk, hogy az útvonal valóban megfelel a feltételnek. A szakaszon szerkesztés szerint rajta van . Jelöljük az -vel -n áthúzott párhuzamos és metszéspontját -gal. Ekkor az trapéz átlóinak metszéspontja pl. az átlót ‐ amint föntebb láttuk ‐ arányban osztja, tehát egybeesik az ponttal. Mivel szerkesztés szerint egyenlő szárú háromszög, így is, amiből következik, hogy szimmetrikus trapéz, s így a szárak meghosszabbításának a metszéspontja is ‐ ami a pont ‐ a szimmetriatengelyre esik. Ez azt jelenti, hogy az háromszög egyenlő szárú: .
egyértelműen szerkeszthető és mindig létezik. -re 2, 1, vagy 0 megoldást kapunk. -ből szerkesztése ismét egyértelmű és mindig létezik, mert a feladat szerint .
Bellay Ágnes (Budapest, Fazekas M. Gyak. Gimn. III. o. t.)
II. megoldás. Legyen (az eddigi jelöléseket megtartva) és vetülete -re , ill. , -re , ill. , végül és vetülete -re , ill. . Így az átmérőjű Thalész‐körön van. Másrészt | |
eszerint megszerkeszthetjük -nek -től való távolságát, és ebből még egy mértani helyet kapunk számára. Így , majd belőle megszerkeszthető. (A fenti egyenesnek -vel való metszéspontját -rel jelölve -nek -n levő metszéspontjára .)
A szerkesztés helyességének bizonyítását mellőzve csupán azt említjük, hogy a megoldások száma innen is 2, 1 vagy 0.
Máté Eörs (Szeged, Radnóti M. Gimn. III. o. t.)
Megjegyzés. A megoldók többsége -t a és alappontokhoz és a arányhoz tartozó Apollóniusz‐körrel metszette ki -ből.
Ugyanis a fenti jelölésekkel 5 dolgozat pedig bonyolult számítások alapján adott szerkesztést.
Ehhez még az háromszög egyenlő szárú voltát sem használtuk fel. |
|
 PDF |
PDF |  MathML
MathML