Kezdőlap


Feladat:	1109. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Benczúr A. , Bollobás B. , Csipka L. , Demendy Zoltán , Farkas Z. , Gagyi Pálffy A. , Gálfi l. , Huber T. , Kéry G. , Kóta J. , Krámli A. , Kunszt Z. , Lehel J. , Máté A. , Máté E. , Molnár E. , Nagy Ernő , Nováky B. , Opálény M. , Ratkó I. , Seprődi L. , Simonovits M. , Sonnevend Gy. , Szepesvári I. , Vesztergombi Gy. , Vincze I. , Zalay M.
Füzet:	1962/január, 42 - 43. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Alakzatba írt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1961/április: 1109. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$H$ -val együtt az $A D$ átlóra a körülírt és a beírt kör is tükrös, tehát az $O$ és $M$ középpontok $A D$ -n vannak. Legyen a körök sugara $R$ , ill. $r$ , és $O M = c$ . Feltehetjük, hogy a csúcsok úgy vannak megbetűzve, hogy $M$ az $A O$ szakaszon van ‐ esetleg éppen $O$ -ban. Így $A M = R - c$ , $D M = R + c$ . Legyen a beírt kör érintési pontja 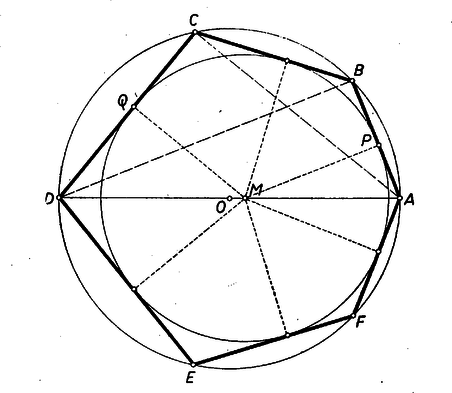$A B$ -n $P$ , $C D$ -n $Q$ .

Ekkor az

A B D

és

A P M

, valamint

D C A

és

D Q M

derékszögű háromszögek hasonlóságából, továbbá az

A P M

és

D Q M

derékszögű háromszögekből:

\begin{matrix} \frac{A B}{A D} = \frac{A P}{A M} = \frac{\sqrt[]{{(R - c)}^{2} - r^{2}}}{R - c}, \frac{C D}{A D} = \frac{Q D}{M D} = \frac{\sqrt[]{{(R + c)}^{2} - r^{2}}}{R + c} . \end{matrix}

Ezeket a közölt összefüggésnek

A D

-vel végigosztott alakjába helyettesítve a kívánt összefüggés:

\begin{matrix} \frac{\sqrt[]{{(R - c)}^{2} - r^{2}}}{R - c} + \frac{\sqrt[]{{(R + c)}^{2} - r^{2}}}{R + c} = 1. \end{matrix}

Négyzetgyöktől mentes alakot kapunk az összefüggésre, ha azt ‐ közbülső rendezések után ‐ kétszer négyzetre emeljük:

\begin{matrix} 3 {(R^{2} - c^{2})}^{4} - 4 {(R^{2} - c^{2})}^{2} (R^{2} + c^{2}) r^{2} - 16 R^{2} c^{2} r^{4} = 0. \end{matrix}

Demendy Zoltán (Budapest, XVIII. ker. Hengersor úti Gimn., III. o. t.)