Kezdőlap


Feladat:	1108. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Békési G. , Benczúr András , Bollobás Béla , Csipka L. , Demendy Z. , Farkas Zoltán , Fritsch I. , Fukker G. , Gagyi Pálffy A. , Gálfi László , Kiss Tünde , Kóta J. , Kovács I. , Krámli András , Kunszt Z. , Major J. , Máté A. , Máté E. , Molnár Emil , Náray-Szabó G. , Nováky Béla , Opálény M. , Pór András , Ratkó István , Sebestyén Z. , Seprődi L. , Simonovits Miklós , Sonnevend Gy. , Szegő K. , Szepesvári I. , Vesztergombi György , Zalán P.
Füzet:	1962/január, 40 - 42. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Körülírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1961/április: 1108. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltehetjük, hogy $P$ az $A B C$ háromszög csúcsaitól különböző pontja $k$ -nak, ugyanis az ellentétes esetben az állítás nyilvánvalóan igaz: mindkét szorzat értéke 0. Megmutatjuk, hogy $P$ -nek bármelyik oldaltól való távolsága mértani középarányos az illető oldal végpontjaiban húzott érintőktől való távolságoknak, pl. 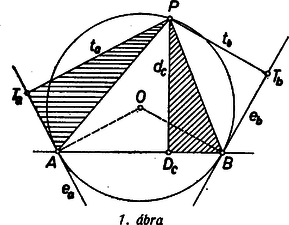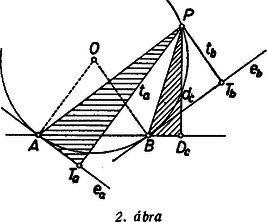$d_{c}^{2} = t_{a} t_{b}$ .

Legyen

P

vetülete az

A B

oldalon

D_{c}

, az

A

csúcsbeli

e_{a}

érintőn

T_{a}

, a

B

-beli

e_{b}

érintőn

T_{b}

. Egyelőre feltesszük, hogy

T_{a}

nem azonos

A

-val, és

D_{c}

nem azonos

B

-vel. Ekkor a

P A T_{a}

és

P B D_{c}

derékszögű háromszögek hasonlók, mert

P A T_{a}

, ill.

P B D_{c}

hegyesszögük egyenlő. Ugyanis a

P A T_{a}

hegyesszög

k

-ban kerületi szög, és így szárai között a kisebb

P A

ív fekszik. A

P B D_{c}

szög a

P B A

kerületi szöggel vagy azonos ‐ ha ti.

D_{c}

B A

félegyenesen van ‐, vagy annak kiegészítő szöge ‐ ha

D_{c}

A B

oldal

B

-n túli meghosszabbításának pontja (1-2. ábra). A

P B A

szög az előbbi esetben hegyesszög, az utóbbiban tompaszög, ezért szárai között

k

-ból a kisebb, ill. nagyobb

P A

ív fekszik. Ezért az első esetben

P B A

egyenlő a

P A T_{a}

szöggel, a másodikban pedig annak kiegészítő szöge. Így a

P B D_{c}

hegyesszög valóban mindig egyenlő a

P A T_{a}

szöggel.
A bebizonyított hasonlóság alapján

\begin{matrix} \frac{P T_{a}}{P D_{c}} = \frac{t_{a}}{d_{c}} = \frac{P A}{P B} . \end{matrix}

(1)

Ugyanígy a

P B T_{b}

és

P A D_{c}

derékszögű háromszögek hasonlóságából

\begin{matrix} \frac{P T_{b}}{P D_{c}} = \frac{t_{b}}{d_{c}} = \frac{P B}{P A}, \end{matrix}

(2)

végül (1) és (2) összeszorzásából

\begin{matrix} \frac{t_{a} t_{b}}{d_{c}^{2}} = 1, azaz t_{a} t_{b} = d_{c}^{2} . \end{matrix}

(3)

Ezt akartuk bizonyítani.
A fentebbi

P A T_{a}

és

P B D_{c}

derékszögű háromszögek akkor és csak akkor fajulnak el a

P A

, ill.

P B

egyenesszakasszá, ha

P

k

-nak

A

-val átellenes pontjában van (3. ábra). Ekkor a

P A B

derékszögű háromszög hasonló

P B T_{b}

-höz, mert

A

-nál, ill.

B

-nél levő szögük a

P B

íven fekvő kerületi szög, ennélfogva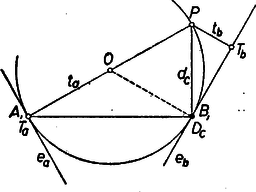

\begin{matrix} P A : P B = P B : P T_{b}, \end{matrix}

amiből közvetlenül kapjuk (3)-at. Hasonlóan egyszerű a bizonyítás akkor is, ha

P

B

-vel átellenes pontban van.

3. ábra

Most már (3)-at és a betűk megfelelő felcserélésével adódó

\begin{matrix} t_{b} t_{c} = d_{a}^{2}, t_{c} t_{a} = d_{b}^{2} \end{matrix}

egyenlőségeket összeszorozva

\begin{matrix} t_{a}^{2} t_{b}^{2} t_{c}^{2} = d_{a}^{2} d_{b}^{2} d_{c}^{2} . \end{matrix}

Innen pedig négyzetgyökvonással, és figyelembe véve, hogy a szóban forgó távolságok nem lehetnek negatívok, a bizonyítandó állítást kapjuk.

Megjegyzések. 1. Több dolgozat csak 1 ‐ 1 konkrét helyzetre bizonyította a felhasznált hasonlóságot és ebben esetenként más-más szögegyenlőségre hivatkozott. Közülük néhányan legalább említették, hogy más helyzetben a bizonyításban lényegtelen módosítások szükségesek.
2. Akkor is több eset szétválasztására van szükség, ha (3)-at egyetlen háromszög-pár:

P T_{a} D_{c}

és

P D_{c} T_{b}

hasonlósága alapján kívánjuk bizonyítani, pl. a

P D_{c} A T_{a}

és

P T_{b} B D_{c}

húrnégyszögek felhasználásával.
3. A (3) összefüggést az 1961. évi Országos Középiskolai Matematikai Verseny II. fordulója 2. feladatának¹ eredményéből is kiolvashatjuk.

¹Lásd K. M. L. 24 (1962) 2. o.