Feladat: 1100. matematika feladat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Vogronics László 
Füzet: 1962/január, 27 - 28. oldal  PDF  |  MathML 
Témakör(ök): Mértani helyek, Hossz, kerület, Feladat
Hivatkozás(ok):Feladatok: 1961/március: 1100. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az adott téglalap ABCD és AB=a, BC=b. Feltesszük, hogy c ugyancsak adott szakasz.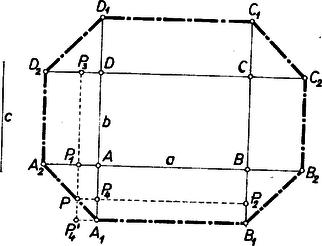
Az AB és CD egyenesek közötti síksáv belső és határpontjaira nézve az ezen egyenesektől mért két távolság összege nyilvánvalóan b. A sávon kívüli félsíkok pontjaira pedig b-nél annyival több ez az összeg, mint a pont és a félsík határegyenese közti távolság 2-szerese. Hasonló megállapítások érvényesek az AD és BC egyenesek közti síksáv, ill. az ezeken kívüli két félsík pontjaira, ha az AD és BC-től mért távolságok összegét tekintjük, csupán b helyett a-t kell írnunk.

 
 

Ezek szerint a téglalap belsejében és oldalszakaszain levő pontokra nézve a négy oldaltól mért távolságok összege a+b, itt tehát nem lehet pontja a keresett mértani helynek. Az AB és CD oldalakhoz csatlakozó félsíksáv pontjai közül azok, és csak azok felelnek meg a követelménynek, amelyekre az AB és CD-től számított távolságok összege b+c, vagyis amelyeknek távolsága AB, ill. CD-től c/2. Ezek nyilván azoknak az A1B1 és C1D1 szakaszoknak összes pontjai, amelyekre A1 és D1 az AD oldal A-n, ill. D-n túli meghosszabbításán van, B1, C1 pedig a BC oldal megfelelő két meghosszabbításán, és AA1=BB1=CC1=DD1=c/2.
Ugyanígy az AD, BC oldalakhoz csatlakozó félsíksávokban az ábra A2D2, B2C2 szakaszainak pontjai ‐ és csak ezek ‐ tartoznak a mértani helyhez.
Legyen P egy a BAD szög csúcsszög-tartományáhan fekvő és a követelménynek eleget tevő pont, vagyis amelyre
PP1+PP2+PP3+PP4=a+b+c,(1)


ahol P1, P2, P3, P4 a P vetülete az AB, BC, CD, DA egyenesen. Figyelembe véve, hogy PP2=PP4+P4P2=PP4+a és PP3=PP1+P1P3=PP1+b, ‐ (1) így alakul:
PP1+PP4=c2.
Mérjük rá PP4-et P1P-nek P-n túli meghosszabbítására, és legyen a végpont P4. Így
P1P'4=P1P+PP'4=P1P+PP4=c2=AA1,
ezért az AP1P'4A1 négyszög téglalap, a PP'4A1P4 négyszög pedig négyzet, tehát PA1A∢=PA1P4∢=45∘=A2A1A∢, ‐ ugyanis AA1A2 egyenlő szárú derékszögű háromszög. Eszerint P az A1A2 szakasz pontja.
Viszont P-vel az A1A2 szakasz bármely belső pontját jelölve meggondolásunk megfordítása mutatja, hogy P megfelel a követelménynek, tehát a mértani helynek a BAD szög csúcsszögtartományában levő része az A1A2 szakasz.
Hasonlóan nyilvánvaló, hogy a mértani helynek az ABC, BCD, CDA szög csúcsszögtartományába eső része a B1B2, C1C2, D1D2 szakasz, tehát a mértani hely az A1B1B2C2C1D1D2A2 nyolcszög kerülete.
 
 Vogronics László (Pécs, Zipernovszky K. gépip. t., III. o. t.)