| Feladat: | 1099. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bollobás Béla , Juhász István , Molnár Emil , Nováky Béla , Szőts Miklós | ||
| Füzet: | 1962/január, 24 - 27. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Ceva-tétel, Szögfelező egyenes, Terület, felszín, Számtani-mértani egyenlőtlenségek, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1961/március: 1099. matematika feladat | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.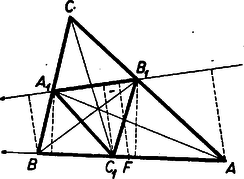 I. megoldás. A 871. feladatban1 az szakaszokat, majd az , , szögek szinuszát kifejeztük az háromszög , , oldalaival és területével. Ezekkel felírtuk az , és háromszögek területét. Végül ezek összegének -ből való levonásával azt találtuk, hogy az háromszög területe:
, , pozitív számok, ezért a két pozitív szám számtani és mértani közepének ismert nagyságviszonya szerint Ezzel az állítást igazoltuk. Egyenlőség csak mellett, tehát szabályos háromszög esetében áll fenn. Szőts Miklós (Budapest, Corvin Mátyás g. IV. o. t.) 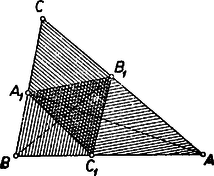 Legyen a -ből húzott magasság . Ezzel és -nek -től való , távolságára
-nek -től való távolsága egyenlő és ugyancsak -től mért távolságainak számtani közepével, ezért
Eszerint , vagyis . Ezt kellett bizonyítanunk. Egyenlőség akkor és csak akkor áll, ha mindegyik szögfelező a szemben fekvő oldalt a felezőpontjában metszi, vagyis ha az eredeti háromszög szabályos. Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. IV. o. t.) Juhász István (Budapest, Madách I. g. IV. o. t.) és Nováky Béla (Budapest, I. István g. III. o. t.) dolgozatából 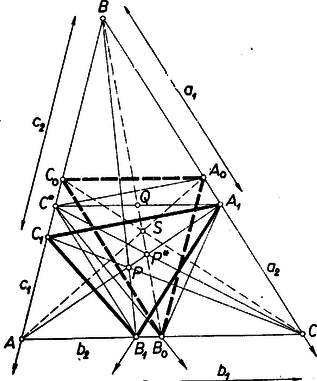 Legyen , , , , , . Ekkor a területek fenti jelölésével ennélfogva állításunk a következő: Ceva tétele szerint , ezért a számláló így alakítható: Eredményünk érvényes az eredeti feladatra, mert a szögfelezők egy pontban metszik egymást. Ezzel az állítást bebizonyítottuk. Molnár Emil (Győr, Révai M. g. IV. o. t.) Juhász István (Budapest, Madách I. g. IV. o. t.) Így a szakaszon, pedig az szakaszon van. Ha egybeesnek ill. -lal, akkor azonos -sel, tehát is -lal és az háromszög területe az háromszögének negyedrésze. Ha és közül legalább az egyik különbözik a megfelelő oldal felezőpontjától, akkor az egyenes az oldal -n túli meghosszabbítását metszi, így ha -et távolítjuk az oldal mentén -tól (-et és -et változatlanul hagyva, tehát nem ügyelve arra, hogy , , továbbra is egy ponton menjen keresztül), akkor az egyenestől való távolsága növekszik. Legyen az -en át -vel párhuzamosan húzott egyenes metszéspontja az oldallal. Megmutatjuk, hogy az trapéz és átlóinak metszéspontja a súlyvonalra esik. felezi az szakaszt. Legyen a metszéspontjuk . Ekkor és hasonló háromszögek (megfelelő szögeik egyenlők), s így . De tudjuk (az és háromszögek hasonlóságából), hogy ugyanilyen arányban osztja -et a átlóval való metszéspont is, tehát a pontban, s így a súlyvonalon metszi -et, ‐ és ezt állítottuk. Most már közbeiktatott háromszögek felhasználásával összehasonlíthatjuk az és háromszögek területét. Ha azonos -vel, akkor azonos -gyel, s így az háromszög ugyanaz, mint . Ha a szakasz belsejében van, akkor egyszersmind a háromszögben van, s így a szakaszhoz tartozik, tehát messzebb van -tól, mint , s így az -től való távolsága nagyobb, mint -é; ennek folytán az háromszög területe kisebb, mint -é, az utóbbi pedig megegyezik az háromszögével, mert párhuzamos -vel. Ez a háromszög egybe eshet -lal (ha az szakaszon s így az pontban van). Ha különbözik tőle, akkor a szakasz belsejében van, s így az szakasz belsejében. Ekkor a oldal -n túli meghosszabbítását metszi, így közelebb van -hoz, mint . Így ‐ a háromszögek területét ugyanúgy jelölve, mint a háromszögeket magukat ‐ azt nyertük (tekintettel arra is, hogy ), hogy Ezzel állításunkat igazoltuk. Az első lépésben csak akkor nem nagyobbítunk, ha a súlyvonalon van, a harmadikban pedig akkor, ha az súlyvonalon is van, tehát egyenlőség csak akkor állhat, ha a háromszög súlypontja, és ekkor valóban az egyenlőségjel érvényes. 1K. M. L. 17 (1958) 7. o. |