Kezdőlap


Feladat:	1087. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Benczúr A. , Bollobás B. , Bornes Klára , Demendy Z. , Farkas Z. , Fritsch I. , Gagyi Pálffy A. , Gálfi l. , Gáspár R. , Gergely M. , Hegedűs J. , Homitzky L. , Horváth T. , Huber T. , Juhász I. , Katona Mária , Kéry Gerzson , Knuth E. , Kóta J. , Kovács I. (Békés) , Kunszt Z. , Lehel J. , Máté A. , Máté E. , Mócsi Z. , Molnár E. , Nagypál B. , Náray-Szabó G. , Opálény M. , Pór A. , Rátkai János , Ratkó I. , Rédei Gy. , Seprődi L. , Simonovits M. , Somogyi Károly , Sonnevend Gy. , Székely J. , Szepesvári I. , Tistyán P. , Vesztergombi Gy. , Vincze I. , Zalay M.
Füzet:	1961/november, 135 - 137. oldal		PDF \| MathML
Témakör(ök):	Számsorozatok, Feladat
Hivatkozás(ok):	Feladatok: 1961/február: 1087. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a sorozat tagjait rendre $a_{1}$ , $a_{2}$ , $...$ , $a_{n}$ -nel, vagyis $a_{k} = a k^{2} + b k + c$ . Az előírt összehasonlítások céljára képezzük egy tetszés szerinti szomszédos tagpárnak, $a_{k + 1}$ és $a_{k}$ -nak $d_{k}$ különbségét, ahol $k = 1$ , 2, $...$ , $n - 1$ .

\begin{matrix} d_{k} = a_{k + 1} - a_{k} = [a {(k + 1)}^{2} + b (k + 1) + c] - (a k^{2} + b k + c) = a + b + 2 a k . \end{matrix}

Vagy, arra tekintettel, hogy alább ismételten fellép a

3 a + b

kifejezés:

\begin{matrix} d_{k} = (3 a + b) + 2 a (k - 1) . \end{matrix}

(1)

Most már az

α)

esetben, mivel

a > 0

és

k - 1 ≧ 0

, minden szóba jövő

k

-ra

d_{k} > 0

, vagyis

a_{k + 1} > a_{k}

, eszerint

a_{2}

-től kezdve valóban minden tag nagyobb az előtte állónál (

a_{1}

mindvégig csak azért kivétel, mert nincs mihez hasonlítani).
A

β)

esetben

d_{k} = 2 a (k - 1)

, sohasem negatív, de

k = 1

esetén

d_{1} = 0

. Ezért

a_{2} = a_{1}

, és minden

k > 1

értékre

a_{k + 1} > a_{k}

. Ez megfelel a feladat állításának.
A

γ)

eset feltételét két egyenlőtlenségre bontjuk:

\begin{matrix} b < - 3 a, vagyis 3 a + b < 0, és \\ - (2 n - 1) a < b, vagyis (2 n - 1) a + b > 0. \end{matrix}

Így (1)-ből

k = 1

-re

d_{1} = 3 a + b < 0

, tehát

a_{1} > a_{2}

. Viszont

k = n - 1

-re

d_{n - 1} = 2 a (n - 2) + 3 a + b = (2 n - 1) a + b > 0

, tehát

a_{n} > a_{n - 1}

. Ezek szerint az

a_{2}

és

a_{n - 1}

tagok kisebbikére teljesül az idevágó állítás, ugyanis ez a tag

a_{1}

és

a_{n} - a

legkisebb és a legnagyobb sorszámú tagok ‐ mindegyikénél kisebb.

n = 3

, vagyis

n - 1 = 2

a_{n - 1} \equiv a_{2}

esetén

a_{2}

megfelel, más tagról nem is lehet szó.
A hátralevő esetek céljára

d_{k}

-t úgy alakítjuk, hogy külön tagként tartalmazza a feltételek bal oldalán álló kifejezést:

\begin{matrix} d_{k} = [(2 n - 1) a + b] + 2 a (k + 1 - n) . \end{matrix}

(2)

Így a

δ)

esetben

d_{k} = 2 a (k + 1 - n)

, és ez nem lehet pozitív, mert a zárójel negatív, vagy 0. Valóban,

k = n - 1

mellett

d_{n - 1} = a_{n} - a_{n - 1} = 0

, vagyis

a_{n} = a_{n - 1}

, és

k < n - 1

mellett

d_{k} < 0

, tehát

a_{k + 1} < a_{k}

, vagyis minden tag vagy kisebb az előtte állónál, vagy egyenlő avval, valóban nem nagyobb.
Végül az

ε)

esetben (2) első szögletes zárójele negatív, a második nem pozitív, így összegük negatív, minden

k

-ra

d_{k} < 0

a_{k + 1} < a_{k}

, az állításnak megfelelően.

Somogyi Károly (Bonyhád, Petőfi S. g. III. o. t.)

Megjegyzés. (1) szerint a

d_{k}

különbségek

n - 1

tagú,

2 a

különbségű számtani sorozatot alkotnak, a kezdő tag

3 a + b

. Mivel

2 a

pozitív, azért ez a sorozat minden esetben növekedő. Az

α

β

...

ε

) feltételek burkoltan ezen sorozat tagjainak előjelét adták meg, pontosabban az

α)

és

β)

esetben az első tag, a

δ)

és

ε)

esetben az utolsó tag, a

γ)

esetben pedig az első és az utolsó tag előjelét (a

β)

és

δ)

esetben azt, hogy az említett tag értéke 0). Ebből és a sorozat növekedő voltából állapíthattuk meg mindegyik esetben a

d

-sorozatban előforduló előjeleket, majd erre támaszkodva mondhattuk ki, hogy az eredeti sorozat az öt esetben rendre mindvégig növekvő, ‐ az első két tag kivételével növekvő, de a kivett két tagra sem csökkenő, tehát nem csökkenő, ‐ csökkenő, majd növekvő, ‐ az utolsó két tag kivételével csökkenő, de ott sem növekvő, tehát nem növekvő, ‐ ill. mindvégig csökkenő.

Kéry Gerzson (Sopron, Széchenyi I. g. III. o. t.)

II. megoldás. A kérdéses számsorozat tagjait az

y = a x^{2} + b x + c

másodfokú függvénynek az

x = 1

, 2,

...

n

egész helyeken felvett értékei adják meg. E függvény menetét jól ismerjük, ezért a sorozat szomszédos tagjai közti nagyságviszonyokat kiolvashatjuk a függvény grafikonjából. A függvényt

\begin{matrix} y = a [{(x + \frac{b}{2 a})}^{2} + \frac{4 a c - b^{2}}{4 a^{2}}] \end{matrix}

(3)

alakban írva látjuk, hogy legkisebb értékét az

x = - b / 2 a

helyen veszi fel, ezen az abszcisszán van a grafikont adó parabola csúcsa, és az

x = - b / 2 a

egyenes a parabola szimmetriatengelye. Mivel

a > 0

, a parabola ágai felfelé emelkednek, vagyis az

X

-tengelyen balról jobbra haladva a grafikon

x = - b / 2 a

-ig süllyed, onnan tovább emelkedik. Az

x + b / 2 a

összeg abszolút értéke az (

x

y

) pontnak a szimmetriatengelytől való távolságát adja. (3)-ból látjuk, hogy

| x + b / 2 a |

növekedésével

y

is növekszik.
A feltételek alakításával megállapíthatjuk

a - b / 2 a

hányadosnak a

k = 1

, 2, 3,

...

n

sorozat tagjaihoz való nagyságviszonyát, ebből pedig azt, hogy a sorozatunk tagjait ábrázoló (1,

a_{1}

), (2,

a_{2}

...

, (

n - 1

a_{n - 1})

, (

n

a_{n}

) pontok a parabolán a csúcshoz képest hogyan helyezkednek el. Átrendezéssel és osztással a feltételek az ábra bal oldalán feltüntetett alakba írhatók.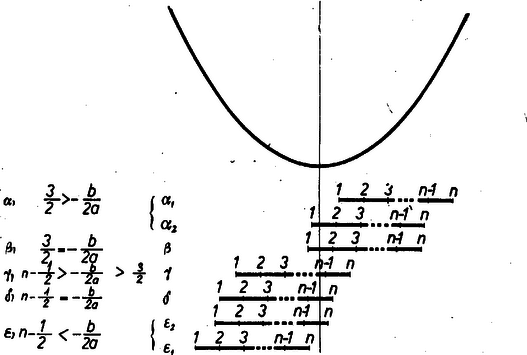

Eszerint a

β

) és

δ

) esetben a parabola tengelye az

X

-tengely 1 és 2, ill.

n - 1

és

n

abszcisszájú pontjai közti szakasz felező merőlegese, tehát a parabola szimmetriája folytán a megfelelő ordinátákra áll:

a_{1} = a_{2}

, ill.

a_{n - 1} = a_{n}

így a

β

) esetben az (1,

a_{1}

) pont kivételével minden pontunk a parabola emelkedő ágán van, az ordináták sorozata növekvő; a

δ

) esetben pedig az (

n

a_{n}

) pont kivételével minden pontunk a süllyedő ágon van, a sorozat csökkenő.
Az

α

) esetben a parabola tengelye balra, az

ε

) esetben pedig jobbra van a

β

), ill.

δ

) esetben említett felező merőlegestől. Ebből nem lehet megállapítani, hogy az (1,

a_{1}

), ill. az (

n

a_{n}

) pont a grafikon melyik ágán van. Azonban az (1,

a_{1}

) pont mindenesetre közelebb van a szimmetriatengelyhez, mint a (2,

a_{2}

) pont, így ordinátája kisebb:

a_{1} < a_{2}

, tehát a számsorozat mindvégig növekedő. Hasonlóan az

ε

) esetben az (

n

a_{n}

) pont közelebb van a tengelyhez, mint (

n - 1

a_{n - 1}

), és ezért

a_{n} < a_{n_{1}}

.
Végül a

γ

) esetben a parabola tengelye jobbra van az

x = 3 / 2

egyenestől, tehát az (1,

a_{1}

) pont a süllyedő ágon van, éspedig a tengelytől távolabb, mint (2,

a_{2}

), és ezért

a_{1} > a_{2}

, másrészt a tengely balra van az

x = n - 1 / 2

egyenestől, és ezért az (

n

a_{n}

) pont az emelkedő ágon van, a tengelytől távolabb, mint (

n - 1

a_{n - 1}

) és ezért

a_{n} > a_{n - 1}

. Így a (2,

a_{2}

) és (

n - 1

a_{n - 1}

) pontok közül a kisebb ordinátájú mind (1,

a_{1}

)-nél, mind (

n

a_{n}

)-nél alacsonyabban van.

Rátkai János (Kisújszállás, Móricz Zs. g. IV. o. t.)