Kezdőlap


Feladat:	1086. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ambrózy György
Füzet:	1961/november, 134 - 135. oldal		PDF \| MathML
Témakör(ök):	Kocka, Térfogat, Gömb és részei, Feladat
Hivatkozás(ok):	Feladatok: 1961/január: 1086. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kocka élének hosszát $e$ -vel jelölve a szóban forgó gömb átmérője egyenlő a kocka két szemben fekvő élének $e \sqrt[]{2}$ távolságával, ugyanis két ilyen élen átmenő átlós síkmetszet téglalap, melynek oldalai az él és a lapbeli átló.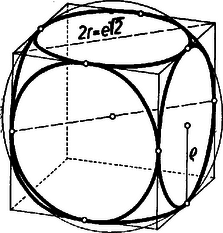

Így a gömb sugara

r = e \sqrt[]{2} / 2

. Eszerint a gömb felülete részben kívül, részben belül van a kockán, mert a lapoknak a középponttól való

d = e / 2

távolsága kisebb

r

-nél, a csúcsok

e \sqrt[]{3} / 2

távolsága viszont nagyobb nála. A gömb a lapokat olyan körökben metszi, amelyek érintik a lapot határoló éleket, tehát sugaruk

ϱ = e / 2

. Így a maradéktestet 6

ϱ

‐sugarú körlap és a gömbfelület 8 háromszög alakú részlete határolja.
Célszerűbb fordítva azt mondanunk, hogy a kocka lapjai a gömbfelületből 6 egybevágó gömbsüveget, a gömbtestből pedig 6 egybevágó gömbszeletet metszenek le. A süveg és a szelet magassága

m = r - d = e (\sqrt[]{2} - 1) / 2

, ennélfogva az eltávolított részek együttes felszíne, ill. térfogata:

\begin{matrix} f & = 6 \cdot 2 π r m = 3 (2 - \sqrt[]{2}) π e^{2}, \\ v & = 6 \frac{π m}{6} (3 ϱ^{2} + m^{2}) = \frac{π e (\sqrt[]{2} - 1)}{2} [\frac{3 e^{2}}{4} + \frac{e^{2} (3 - 2 \sqrt[]{2})}{4}] = \\ = \frac{π e^{3}}{4} (\sqrt[]{2} - 1) (3 - \sqrt[]{2}) = \frac{π e^{3}}{4} (4 \sqrt[]{2} - 5) . \end{matrix}

Ezekkel a gömb visszamaradt részének felszíne, ill. térfogata:

\begin{matrix} F_{1} = 4 π r^{2} - f = 2 π e^{2} - 3 (2 - \sqrt[]{2}) π e^{2} = (3 \sqrt[]{2} - 4) π e^{2}, \\ V = \frac{4 π}{3} r^{3} - v = \frac{4 π}{3} \frac{e^{3} \sqrt[]{2}}{4} - \frac{π e^{3}}{4} (4 \sqrt[]{2} - 5) = \frac{π e^{3}}{12} (15 - 8 \sqrt[]{2}) . \end{matrix}

Ezzel a dobókocka térfogatát megkaptuk, felszínét pedig

F_{1}

-nek és a 6 körlap területének összege adja:

\begin{matrix} F = 6 π ϱ^{2} + F_{1} = \frac{3 π}{2} e^{2} + (3 \sqrt[]{2} - 4) π e^{2} = \frac{π}{2} (6 \sqrt[]{2} - 5) e^{2} . \end{matrix}

Az állandókat 4 értékes jegyű tizedes törtekkel megközelítve

V \approx 0, 9651 e^{3}

F = 5, 475 e^{2}

, vagyis

96, 5

, ill.

91, 2 %

-a kocka térfogatának, ill. felszínének.

Ambrózy György (Budapest, Toldy F. g. III. o. t.)