|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Legyenek az négyszögnek az , , , csúcsnál fekvő, szögei , , , , oldalai , , , , átlói , , a köztük levő szög , végül a terület (1. ábra). 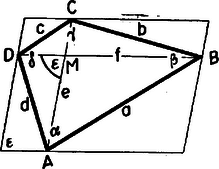 1. ábra
‐ A és , valamint és háromszögpárokból az átlók négyzetére
és innen
Ugyanezen háromszögpárokból a terület 2-szeresére
(1a) és (1b) az és -ra, (2a) és (2b) a és -ra nézve olyan típusú egyenletrendszer, amilyet az 1076. feladatban adott számokkal megoldottunk, ugyanis bármelyik szög koszinuszának és szinuszának együtthatói abszolút értékben egyenlők.
A megoldási eljárás vázolása céljára az együtthatókat egy‐egy új betűvel jelölve két rendszerünk közös általános alakja:
Az 1076/I-beli gondolatmenettel küszöböljük ki -t, felírva azt, hogy és kifejezéseinek négyzetösszege 1-gyel egyenlő. Mindjárt -nel szorozva:
Ilyen típusú egyismeretlenes trigonometriai egyenlet megoldását ugyanott az a) részben láttuk. Ismét új betűkkel általános alakja: A bal oldal egyik tagját különválasztva, majd négyzetre emeléssel egyik függvényére másodfokú egyenletet kapunk:
ahonnan -re, majd (6) alapján -re
Ez esetén -re 2, 1, 0 valós megoldást ad, és ‐ mint az 1076/I. megoldásban láttuk ‐ nincs szükség idegen gyökök eltávolítására. Ezekből (3) és (4) alapján egyértelműen megkapjuk a megfelelő -t.
Ezzel megadtuk az eljárást a szögek kiszámítására. Ezekből az átlók (1) és (2) alapján számíthatók. Végül az átlók hajlásszögére | | (9) |
Ugyanis az átlókkal a csúcsokon át húzott párhuzamosok egy , oldalú és szögű paralelogrammát határoznak meg, és ezt az átlók négy paralelogrammára bontják. Ezek mindegyikének egyik átlója a négyszög egyik oldala, és így területük összegének fele adja a négyszög területét.
Számadatainkkal az , szögpárra , , , . Ezekből céljára , , , tehát 80-nal egyszerűsítve (6), (7) és (8) így alakul: | |
ahonnan , . ‐ A (3) és (4)-nek megfelelő egyenletekből | |
A , szögpárra -val hasonlóan , , , , majd , , , és így , ill. -ból | |
végül | |
Mivel és számítása független és számításától, viszont az összefüggésnek teljesülnie kell, azért az összetartozó értékpárokat próbával kell megállapítanunk.
ezért egyrészt az , pár a , párral, másrészt az , pár a , párral alkot egy megoldást.
Ez a megfelelő párba állítás általában is lehetséges, és az észrevehető összefüggés is mindig fennáll. Ha ugyanis az 1076/II. megoldáshoz főzött megjegyzés eljárásával az (1a), (1b), ill. (2a), (2b) rendszerekből kiszámítjuk -t, -t, akkor egyrészt mindegyikre egyetlen értéket kapunk, másrészt ez a két érték egyenlő. Valóban, az egyenletpárokat négyzetre emelve és összeadva
és innen, csekély átalakítással
Számadatainkkal .
Most már az átlókra (1) és (2)-ből
amiből , ; , .
Innen (9) céljára | |
és így , amiből az átlók közti hegyes szög mindkét megoldásra .
Eredményeinket összefoglalva
A második megoldás B-nél homorú szögű négyszöget ad (2. ábra), az AC átló a négyszögön kívül fekszik, a négyszög területét az ACD és ACB háromszögek területének különbsége adja. 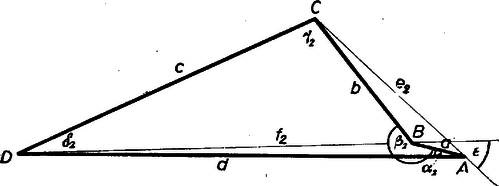 2. ábra
(2b) így is érvényes, ekkor ugyanis sinβ negatív.
| Dömötör Gyula (Szeged, Radnóti M. g. IV. o. t.) |
| Nyárasdy Zsófia (Budapest, Ságvári E. gyak. lg. IV. o. t.) |
| Nováky Béla (Budapest, I. István g. III. o. t.) |
II. megoldás. A négyszög területe egyenlő az ACB és ACD háromszögek területének összegével. Ez utóbbiakat a Heron‐képlet felhasználásával az oldalakkal és az AC=e átlóval kifejezve egyenletet kapunk e-re (4-gyel szoroztunk):
4t=(a+b+e)(a+b-e)(e+a-b)[e-(a-b)]++(c+d+e)(c+d-e)(e+c-d)[e-(c-d)]==[(a+b)2-e2][e2-(a-b)2]+[(c+d)2-e2][e2-(c-d)]2.
Az egyik gyökös kifejezést különválasztva négyzetre emelés után e4 kiesik, és csak egy gyökös kifejezés marad az egyenletben. Ismét különválasztással négyzetre emelés után e2-re másodfokú egyenletet kapunk. ‐ A számadatokkal
(16-e2)(e2-4)+(196-e2)(e2-4)=40,-e4+200e2-784=1600-80(16-e2)(e2-4)-e4+20e2-64,4(16-e2)(e2-4)=116-9e2,-16e4+320e2-1024=13456-2088e2+81e4,97e4-2408e2+14480=0,
amiből a fenti értékek adódnak.
Hasonlóan számítva f-et, a szögek a részháromszögekből koszinusz tétellel számíthatók. Számíthatók az átlókkal kettévágott szögek részei is, pl. a BAC és DBA szögek és ezek összege a BMC szög. Csak azok az e, f összepárosítások megfelelők, amelyekkel az ABD háromszögből számított BAD∢ egyenlő az ABC és ADC-ből számított BAC és DAC szögek összegével, ill. különbségével.
| Zalán Péter (Aszód, Petőfi S. g. III. o. t.) |
Lásd ezen számban, 119. o. Az előjelek is mindkét rendszerben az egyik szögre egyenlők, a másikra ellentétesek; ez azonban lényegtelen, hiszen pl. α és γ ezen megkülönböztetett szerepe (1a)-nak (-1)-gyel való szorzásával felcserélődik. |
 PDF |
PDF |  MathML
MathML 
