Kezdőlap


Feladat:	1084. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zs. , Békési G. , Benczúr A. , Bollobás B. , Butor L. , Csipka L. , Dömötör Gy. , Gálfi l. , Grüner Gy. , Juhász I. , Katona Mária , Kéry G. , Knuth E. , Kóta J. , Kunszt Z. , Lippai P. , Máté A. , Molnár Emil , Nagy Csaba , Nagy Ernő , Opálény M. , Pór A. , Simonovits M. , Szegö Károly , Szidarovszky Ágnes , Szidarovszky F. , Vesztergombi Gy. , Vincze I.
Füzet:	1961/december, 203 - 205. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1961/január: 1084. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. A szokásos jelölésekkel a feltétel $b = 2 \sqrt[]{a c}$ , azaz $b^{2} = 4 a c$ . Feltehetjük, hogy $a < c$ , ugyanis $a = c$ mellett $b = 2 a = a + c$ , vagyis a háromszög egyenlőtlenség nem teljesül. Legyen az $A C$ oldal felezőpontja $F$ , a $B$ -ből húzott magasság talppontja $B'$ ‐ ekkor $B F = s_{b}$ , $B B' = m$ ‐, a vizsgálandó hegyes szög 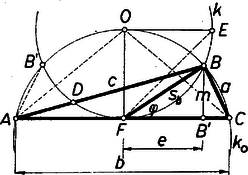$B F C ∢ = φ$ , végül $F B' = e$ .

1. ábra

B B' A

B B' C

és

B B' F

derékszögű háromszögekből:

\begin{matrix} c^{2} = m^{2} + {(\frac{b}{2} + e)}^{2}, & (1) \\ a^{2} = m^{2} + {(\frac{b}{2} - e)}^{2}, & (2) \\ m^{2} + e^{2} = s_{b}^{2} . & (3) \end{matrix}

Írjuk (3) felhasználásával (1) és (2)-t így:

\begin{matrix} c^{2} = (m^{2} + \frac{b^{2}}{4} + e^{2}) + b e = (s_{b}^{2} + \frac{b^{2}}{4}) + b e, & (1') \\ a^{2} = (m^{2} + \frac{b^{2}}{4} + e^{2}) - b e = (s_{b}^{2} + \frac{b^{2}}{4}) - b e, & (2') \end{matrix}

és szorozzuk össze a megfelelő oldalakat:

\begin{matrix} c^{2} a^{2} = \frac{b^{4}}{16} = {(s_{b}^{2} + \frac{b^{2}}{4})}^{2} - b^{2} e^{2} = s_{b}^{4} + \frac{b^{4}}{16} + \frac{b^{2}}{2} (s_{b}^{2} - 2 e^{2}), \\ \frac{b^{2}}{2} (e^{2} - m^{2}) = s_{b}^{4} . & (4) \end{matrix}

A bal oldalnak pozitívnak kell lennie, tehát

e > m

. Így a

B B' F

derékszögű háromszögben a

B B'

befogóval szemben levő

φ

szög a kisebb hegyes szög, s így

φ < 45^{\circ}

. Ezt kellett bizonyítanunk.
2. Ha az

A B C

háromszög hegyesszögű, akkor a

B

csúcs kívül van az

A C

átmérőjű körön, tehát

s_{b} > b / 2

, továbbá a

B'

talppont az

F C

szakasz belsejében van, tehát

e < b / 2

. Levonva (3)-ból (4)-nek

2 / b^{2}

-szeresét, az első követelmény szerint

\begin{matrix} 2 m^{2} = s_{b}^{2} [1 - 2 {(\frac{s_{b}}{b})}^{2}] < s_{b}^{2} {[1 - 2 (\frac{1}{2})}^{2}] = \frac{s_{b}^{2}}{2}, \end{matrix}

és így

\begin{matrix} m < \frac{s_{b}}{2}, sin φ = \frac{m}{s_{b}} < \frac{1}{2}, φ = 30^{\circ} . \end{matrix}

Ahhoz, hogy

φ

-re alsó korlátot kapjunk, (4)-et átalakítjuk, beírva az

e = s_{b} cos φ

m = s_{b} sin φ

összefüggést. Ekkor

s_{b}^{2}

-nel átosztva kapjuk, hogy

\begin{matrix} \frac{b^{2}}{2} (cos^{2} φ - sin^{2} φ) = \frac{b^{2}}{2} cos 2 φ = s_{b}^{2} . \end{matrix}

(5)

Így az

e < b / 2

feltételből, felhasználva a

cos^{2} φ = (1 + cos 2 φ) / 2

összefüggést és (5)-öt

\begin{matrix} e^{2} = s_{b}^{2} cos^{2} φ = \underset{̲}{\frac{s_{b}^{2}}{2} (1 + cos 2 φ) <} \frac{b^{2}}{4} = \underset{̲}{\frac{s_{b}^{2}}{2 cos 2 φ}} . \end{matrix}

Innen az aláhúzott részben egyszerűsítéssel és a pozitív

cos 2 φ

-vel átszorozva az egyenlőtlenség iránya nem változik:

\begin{matrix} cos^{2} 2 φ + cos 2 φ - 1 < 0. \end{matrix}

A bal oldal akkor válik 0-vá, ha

2 cos 2 φ = - 1 \pm \sqrt[]{5}

, ennek alapján a bal oldalt szorzattá alakítva

\begin{matrix} (cos 2 φ + \frac{1 + \sqrt[]{5}}{2}) (cos 2 φ - \frac{\sqrt[]{5} - 1}{2}) < 0, \end{matrix}

végül mivel az első tényező pozitív:

\begin{matrix} cos 2 φ - \frac{\sqrt[]{5} - 1}{2} < 0, cos 2 φ < \frac{\sqrt[]{5} - 1}{2} \approx 0, 6180, \end{matrix}

azért

2 φ > 51, 8^{\circ}

, és

φ > 25, 9^{\circ}

.
Ezek szerint a feltételt teljesítő hegyesszögű háromszögben

25, 9^{\circ} < φ < 30^{\circ}

Szidarovszky Ágnes (Budapest, Ságvári E. gyak. lg. III. o. t.)

II. megoldás. (a feladat

1

. részére). Tekintsük azt a

k

kört, amely átmegy

B

-n és az

A C

oldalt

F

-ben érinti (1. ábra). Legyen

k

középpontja

O

A B

-vel való második metszéspontja

D

. Ekkor egyrészt a kör szelőjére és érintőjére vonatkozó tétel, másrészt a feltevés alapján

\begin{matrix} {(\frac{A C}{2})}^{2} = A F^{2} = A D \cdot A B = C B \cdot A B, \end{matrix}

ennélfogva

A D = C B

. Legyen

B

tükörképe

A C

felező merőlegesére, vagyis

F O

-ra

B'

, ekkor

B'

k

-n van, továbbá

A B' = C B = A D

. Nem lehet, hogy

D

egybeessék

B'

-vel, mert

D A C ∢ = B A C ∢ < B C A ∢ = B' A C ∢

, ezért

D

és

B'

tükrös pár

O A

-ra. Így

\begin{matrix} D A C ∢ = B' A C ∢ = 2 \cdot O A C ∢ = O A C ∢ + O C A ∢ = 180^{\circ} - A O C ∢, és \\ D A C ∢ + B' A C ∢ = B A C ∢ + B C A ∢ = 180^{\circ} - A B C ∢, \end{matrix}

vagyis

A O C ∢ = A B C ∢

. Ezért

A C

az ugyanazon oldalán levő

O

és

B

pontokból ugyanakkora szögben látszik, tehát

O

rajta van az

A B C

háromszög

k_{0}

körülírt körén. A szimmetria miatt

O

k_{0}

kör

A O C

ívének

A C

-től legtávolabbi pontja, tehát

B

közelebb van

A C

-hoz, mint

O

. Megrajzolva

k

-nak

F C

-vel párhuzamos és egyirányú

O E

sugarát, az

F B

ív kisebb az

F E

negyedkörívnél, és így az ezeken fekvő

B F C ∢ = φ

és

E F C ∢ = 45^{\circ}

kerületi szögekre

φ < 45^{\circ}

. Ezt kellett bizonyítanunk.

Molnár Emil (Győr, Révai M. g. IV. o. t.)

III. megoldás. (a feladat

1

. részére). Mérjük rá a

B C

szakaszt az

A B

oldal

B

-n túli meghosszabbítására, legyen a végpont

C'

. Rajzoljuk meg az

A C C'

háromszög körülírt körét, legyen ez

k'

és a középpontja

K

, továbbá

k'

-nek

B

-n átmenő,

K B

-re merőleges

G H

húrját (2. ábra).

2. ábra

Így

B

felezi a

G H

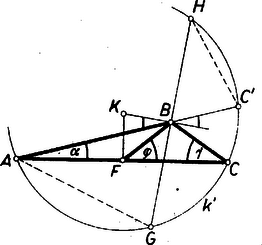húrt, továbbá az

A B G

és

H B C'

háromszögek hasonlók, mert szögeik egyenlők. Ezért

B A : B G = B H : B C'

. Felhasználva ezt,

C'

szerkesztését és a feltevést, nyerjük:

\begin{matrix} B G^{2} = B G \cdot B H = B A \cdot B C' = B A \cdot B C = A F^{2} . \end{matrix}

Innen

B G = A F

, tehát

G H = A C

, és mivel egyenlő hosszú húrok egyenlő távolságra vannak a középponttól, azért

K B = K F

. Így a

K B F

háromszög egyenlő szárú, és

K B F ∢ = K F B ∢ = 90^{\circ} - φ

.
A

B C C'

háromszög egyenlő szárú és

K

rajta van a tengelyén, ezért a

K B

egyenes felezi a

C B C' ∢ = α + γ

szöget. Így

\begin{matrix} A B F ∢ = K B F ∢ - K B A ∢ = 90^{\circ} - φ - \frac{α + γ}{2}, és \\ φ = B F C ∢ = F A B ∢ + A B F ∢ = α + 90^{\circ} - φ - \frac{α + γ}{2}, tehát \\ 2 φ = 90^{\circ} - \frac{γ - α}{2} < 90^{\circ}, és φ < 45^{\circ} . \end{matrix}

Ezzel az állítást bebizonyítottuk.

Szegő Károly (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

Megjegyzés. Az utolsó lépésből hegyes szögű háromszög esetén

φ

-re a következő becslés is adódik:

\begin{matrix} 2 φ = 90^{\circ} - \frac{γ - α}{2} = \frac{2 α + β}{2} > \frac{α + β}{2} > \frac{90^{\circ}}{2}, φ > 22, 5^{\circ} . \end{matrix}

Ez valamivel rosszabb, mint amit az I. megoldásban kaptunk.