Kezdőlap


Feladat:	1073. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Benczúr András , Kóta József , Seprődi László , Székely Jenő
Füzet:	1961/november, 116 - 118. oldal		PDF \| MathML
Témakör(ök):	Háromszög-rácsok geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1960/december: 1073. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹ I. megoldás. A háromszögrács két szomszédos szabályos háromszöge $60^{\circ}$ -os hegyes szögű rombuszt alkot $d$ és $d \sqrt[]{3}$ hosszú átlókkal, melyek egymásra merőlegesek. Tehát a rács minden olyan rácsegyeneséhez², melyen a rácspontok távolsága $d$ , van rá merőleges rácsegyenes is, és ezen a rácsállandó $d \sqrt[]{3}$ . Minden $d$ és $d \sqrt[]{3}$ oldalú rácstéglalap belsejében egy rácspont van, a középpont.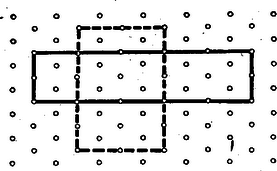

Legyen az elhatárolt téglalap két oldala

b d

és

c d \sqrt[]{3}

, ahol

b

és

c

természetes szám. Így az oldalakon

b

c

b

c

számú fa áll (a körüljárásban mindegyik oldalhoz a kezdőpontot hozzászámítva, a végpontot nem), összesen

2 (b + c)

fa. A határmenti rácspontok szemközti párjait összekötő egyenesek az erdőrészletet

b c

számú,

d

d \sqrt[]{3}

oldalú téglalapra bontják, mindegyik közepén áll egy fa, és az egyenesek

(b - 1) (c - 1)

számú belső metszéspontján egy‐egy fa. Ezzel valamennyi belső fát számításba vettünk, számuk

b c + (b - 1) (c - 1)

. A kérdés tehát ez: van-e olyan

b

c

természetes számpár, amelyre

\begin{matrix} 2 (b + c) = b c + (b - 1) (c - 1) . \end{matrix}

(1)

Innen

\begin{matrix} b = \frac{3 c - 1}{2 c - 3} = 1 + \frac{c + 2}{2 c - 3} . \end{matrix}

Mivel

c + 2

pozitív, azért

2 c - 3

is, tehát

c > 3 / 2

, és mivel

c

egész, így

c ≧ 2

. Másrészt a jobb oldal második tagjára

\begin{matrix} \frac{c + 2}{2 c - 3} = \frac{1}{2} (\frac{2 c + 4}{2 c - 3}) = \frac{1}{2} (1 + \frac{7}{2 c - 3)}) . \end{matrix}

Az utolsó zárójelben a második tagnak páratlan egész számnak kell lennie. Ez 1-nél nagyobb egész

c

-re csak úgy lehet, ha a nevező 1 vagy 7. Innen

c_{1} = 2

és

c_{2} = 5

b_{1} = 5

és

b_{2} = 2

, tehát a követelmény teljesíthető.
A két megoldás alakra különböző, de egyenlő területű erdőrészletet ad, ugyanis a hosszabb oldal

5 : 2 \sqrt[]{3} \approx 1, 44

-szor, ill.

5 \sqrt[]{3} : 2 \approx 4, 33

-szor akkora, mint a rövidebb, a terület viszont mindkétszer

b c d^{2} \sqrt[]{3} = 10 \sqrt[]{3} d^{2}

. (Az ábrából látjuk, hogy egyik oldaluk mentén nyújtva egymásba átvihetők.)

Seprődi László (Budapest, Fáy A. g. III. o. t.)

II. megoldás. Ha (1) szimmetriáját feláldozva

c = b + e

-t írunk (ahol

e

egész),

b

-re másodfokú egyenletet kapunk:

\begin{matrix} 2 b^{2} + 2 (e - 3) b + (1 - 3 e) = 0. \end{matrix}

(2)

Innen

b

csak akkor racionális, ha a diszkrimináns teljes négyzet:

\begin{matrix} 4 {(e - 3)}^{2} - 8 (1 - 3 e) = 4 (e^{2} + 7), \end{matrix}

tehát ha

e^{2} + 7 = f^{2}

, ahol

f

egész. Így

f^{2} - e^{2} = (f - e) (f + e) = 7

, tehát

f - e = 7 / (f + e)

, és az I. megoldáshoz hasonlóan

e = \pm 3

és

| f | = 4

. Most már e két értékével (2)-ből pozitív megoldásként ismét a

b

c = 2

, 5 értékpár adódik.

Benczúr András (Budapest, Fazekas M. gyak. g. III. o. t.)

Megjegyzések. 1. Az (1) összefüggést tagokra bontva, 0-ra redukálva, majd 2-vel szorozva az ismeretleneket tartalmazó tagokat szorzatba foglalhatjuk össze:

\begin{matrix} 2 b c - 3 b - 3 c + 1 = 0, \\ 4 b c - 6 b - 6 c + 2 = 2 b (2 c - 3) - 3 (2 c - 3) - 7 = 0, \\ (2 b - 3) (2 c - 3) = 7. \end{matrix}

Ebből az I. megoldáshoz hasonlóan következtethetünk tovább.

Kóta József (Tatabánya, Árpád g. III. o. t.)

2. Többen abból indultak ki, hogy ,,kicsi'' rácstéglalap belsejében kevesebb a rácspont, mint a kerületén, ,,nagy'' téglalapnál viszont benn van többlet. Megfigyelték ezután a belső rácspontszám növekedését, ha az egyik oldalt növeljük, és így eljutottak egyik, esetleg mindkét megoldáshoz. Dolgozatukból azonban nem derül ki, hogy van-e további megoldás. A feladat kérdésére ezek is igennel válaszoltak, tehát megoldásuk helyes. Ezeket a dolgozatokat 2 pontra értékeltük.
3. Az eredeti kitűzés zárójeles megjegyzésében az

A B C ▵

-et szabályosnak kellett gondolnunk. Rögzített

A

és

B

-vel

A B = d

mellett végtelen sok olyan

C

van, hogy az

A B C ▵

-ben nincs további fa. Mindezekben a

C

-ből húzott magasság

d \sqrt[]{3} / 2

Székely Jenő (Pécs, Nagy Lajos g. IV. o. t.)

¹Az eredeti kitűzés zárójeles megjegyzését töröltük. ‐ Szerk.

²Rácsegyenes minden olyan egyenes, amely két (és akkor már végtelen sok) rácsponton megy át.