Kezdőlap


Feladat:	1069. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Major János , Meleghegyi László
Füzet:	1961/november, 112 - 113. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül sokszögekben, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1960/november: 1069. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{7}$ szabályos hétszög oldala $A_{1} A_{2} = A_{2} A_{3} = ... = A_{7} A_{1} = d_{1}$ , rövidebb átlója $A_{1} A_{3} = A_{2} A_{4} = ... = A_{6} A_{1} = A_{7} A_{2} = d_{2}$ , és hosszabb átlója 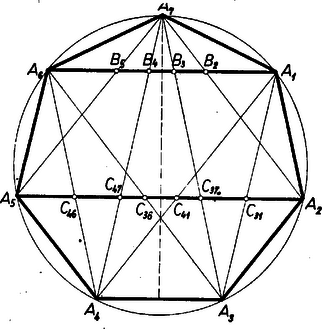$A_{1} A_{4} = A_{2} A_{5} = ... = A_{7} A_{3} = d_{3}$ .

Nyilvánvaló, hogy forgatással bármelyik átló átvihető egy vele egyenlő másik átló helyére úgy, hogy minden csúcs (és ezért minden átló is) egy más csúcs (átló) helyére jut, ezért elegendő az állítást egy

d_{2}

és egy

d_{3}

részeire megmutatnunk. Legyenek ezek

A_{1} A_{6}

, ill.

A_{2} A_{5}

. Ezek a tengelyes szimmetria folytán párhuzamosak egymással és

A_{3} A_{4}

-gyel. Minden más oldallal is egy

d_{2}

és egy

d_{3}

hosszúságú átló párhuzamos, így két alkalmas átlópár paralelogrammát alkot. Alább csak ezt fogjuk felhasználni.
Az

A_{1} A_{6}

átlót csak az

A_{7}

-ből kiinduló

4

átló metszi rendre a

B_{2}

B_{3}

B_{4}

B_{5}

pontokban. Az

A_{2} A_{5}

átlót pedig az

A_{3}

és

A_{4}

-ből kiinduló 8 átló közül 6 metszi (

A_{4} A_{2}

és

A_{3} A_{5}

nem metszik), legyenek a metszéspontok ‐ az őket kimetsző átló végpontjaitól vett indexekkel ‐ rendre

C_{31}

C_{37}

C_{41}

C_{36}

C_{47}

C_{46}

.
Ha meg tudjuk adni

d_{1}

d_{2}

d_{3}

-mal kifejezve minden

B

és minden

C

pontra az

A_{1} A_{6}

, ill.

A_{2} A_{5}

átló egyik végpontjától mért távolságát, ezekből már bármely két

B

közti, és bármely két

C

közti távolságot kivonással megkaphatunk. Sőt elég ezt a távolságot az

A_{7}

-en átmenő tengelyre szimmetrikus (

B_{2}

B_{5}

), (

B_{3}

B_{4}

), (

C_{31}

C_{46}

), (

C_{37}

C_{47}

), (

C_{41}

C_{36}

) pontpárok egyik‐egyik tagjára megadnunk. ‐ Az alábbi felírás mellőzhetővé teszi az éppen felhasznált párhuzamosság megjelölését.

A_{1} B_{4} = A_{3} A_{4} = d_{1}

;

A_{1} B_{5} = C_{41} A_{5} = A_{2} A_{5} - A_{2} C_{41} = A_{2} A_{5} - A_{3} A_{4} = d_{3} - d_{1}

;

A_{2} C_{46} = d_{2}

;

A_{2} C_{37} = A_{1} B_{3} = d_{2} - d_{1}

;

A_{2} C_{41} = A_{3} A_{4} = d_{1}

Ezzel az állítást bebizonyítottuk.

Major János (Budapest, Kandó K. hir. ip. t. II. o. t.)

Megjegyzés. A fenti párhuzamosságokat úgyis felhasználhatjuk, hogy bármely két oldal vagy átló közti szög csak a

180^{\circ} / 7 = ε

-nak egész számú többszöröse lehet. Ebből bizonyos háromszögekre azt kapjuk, hogy egyenlő szárúak, és így ábránkon különböző irányú egyenlő hosszú szakaszokat is megállapíthatunk. Pl.

A_{1} A_{7} B_{4}

-ben

A_{7} A_{1} B_{4} ∢ = A_{7} A_{1} A_{6} ∢ = ε

(

A_{6} A_{7}

íven nyugvó kerületi szög, tehát

360^{\circ} / 7 \cdot 2

A_{1} A_{7} B_{4} ∢ = A_{1} A_{7} A_{4} ∢ = 3 ε

(az

{\hat{A_{1} A}}_{4} = 3 {\hat{A_{6} A}}_{7}

íven), ezért

B_{4} ∢ = 3 ε

, tehát

A_{1} B_{4} = A_{1} A_{7} = d_{1}

. Hasonlóan

A_{3} A_{5} C_{31}

-ből

A_{5} C_{31} = A_{5} A_{2} = d_{2}

. Vagy

A_{3} A_{2} C_{41} ∢ = 2 ε

, és

A_{2} A_{3} C_{41} ∢ = 5 ε / 2

-ből

A_{2} C_{41} = A_{2} A_{3} = d_{1}

Meleghegyi László (Pécs, Nagy Lajos g. IV. o. t.)