Kezdőlap


Feladat:	1068. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bollobás Béla , Fodor János , Kacsó András , Kardeván Péter
Füzet:	1961/november, 110 - 112. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Háromszögek nevezetes tételei, Feuerbach-kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1960/november: 1068. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. Feltesszük, hogy a kérdéses területek 0-tól különbözők. Ez csak akkor nem áll fenn, ha egy csúcs vetülete egybeesik egy másik csúccsal; ilyenkor a 2-ik csúcsnál derékszög van és a 3-ik csúcs vetülete is ide esik, ezért két terület értéke 0, az állítás érvényes, de semmitmondó, mert mindkét oldala 0. Pl. ha $A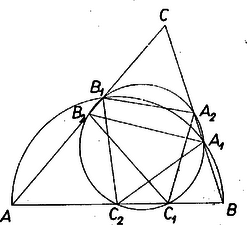_{1} \equiv C$ , akkor $A C B ∢ = 90^{\circ}$ , $B_{1} \equiv C$ , ezért $t_{c 1} = t_{c 2} = 0$ .

I. megoldás.

B_{1}

A B

átmérő fölötti Thalész‐körön van, amelynek középpontja

C_{2}

, ezért

A B_{1} C_{2} ▵

egyenlő szárú. Ugyanez áll

A C_{1} B_{2} ▵

-re. E háromszögekben az alapon fekvő szögek egyike közös (a

B A C ∢

, vagy ha ez tompaszög, akkor a külső szöge), tehát a háromszögek hasonlók. Száraik aránya ‐ a szokásos jelölésekkel ‐

A C_{2} : A B_{2} = c : b

, ezért területeik aránya

c^{2} : b^{2}

. Hasonló eredményt kapunk a további kérdéses háromszögeknek azokról a párjairól, melyekben a közös csúcs

B

, ill.

C

. Most már a

\begin{matrix} \frac{t_{a 1}}{t_{a 2}} = \frac{c^{2}}{b^{2}}, \frac{t_{b 1}}{t_{b 2}} = \frac{a^{2}}{c^{2}}, \frac{t_{c 1}}{t_{c 2}} = \frac{b^{2}}{a^{2}} \end{matrix}

egyenlőségek összeszorzásával kapjuk, hogy az állításban szereplő két szorzat hányadosa 1, a szorzatok egyenlők. Ezt kellett bizonyítanunk.

Fodor János (Miskolc, Földes F. g. III. o. t.)

II. megoldás. Az

A B_{1} C_{2}

és

C B_{1} A_{2} ▵

-ek

A B_{1}

, ill.

C B_{1}

oldalához tartozó magassága egyenlő (a

B B_{1}

magasság fele), ezért területeik aránya egyenlő az alapok arányával. Ugyanezt a

B C_{1} A_{2}

és

A C_{1} B_{2}

, valamint a

C A_{1} B_{2}

és

B A_{1} C_{2}

háromszögpárokra felírva és az egyenlőségeket összeszorozva:

\begin{matrix} \frac{t_{a 1}}{t_{c 2}} \cdot \frac{t_{b 1}}{t_{a 2}} \cdot \frac{t_{c 1}}{t_{b 1}} = \frac{A B_{1}}{C B_{1}} \cdot \frac{B C_{1}}{A C_{1}} \cdot \frac{C A_{1}}{B A_{1}} = \frac{A B_{1}}{A C_{1}} \cdot \frac{B C_{1}}{B A_{1}} \cdot \frac{C A_{1}}{C B_{1}} . \end{matrix}

(1)

B

C

B_{1}

C_{1}

pontok húrnégyszöget határoznak meg, ezért a szögek egyenlősége alapján az

A B_{1} C_{1} ▵

hasonló

A B C ▵

-höz, tehát a jobb oldal első tényezője egyenlő

A B / A C = c / b

-vel. Hasonlóan a további két tényező egyenlő

B C / B A = a / c

-vel ill.

C A / C B = b / a

-val, így a szorzat értékére ismét 1-et kapunk.

Kacsó András (Esztergom, Temesvári P. g. III. o. t.)

Megjegyzések. 1. Az

A_{1}

B_{1}

C_{1}

A_{2}

B_{2}

C_{2}

pontok az

A B C ▵

Feuerbach‐körén vannak. Felírva e körre az

A

B

C

pontokból húzott szelők szorzatának egyenlőségét:

\begin{matrix} A B_{1} \cdot A B_{2} = A C_{1} \cdot A C_{2}, B C_{1} \cdot B C_{2} = B A_{1} \cdot B A_{2}, C A_{1} \cdot C A_{2} = C B_{1} \cdot C B_{2} \end{matrix}

majd ezek szorzatát az

A B_{2} = C B_{2}

B C_{2} = A C_{2}

C A_{2} = B A_{2}

egyenlőségek alapján egyszerűsítve ismét kapjuk, hogy az (1) jobb oldalán álló számlálók szorzata egyenlő a nevezők szorzatával.

Kardeván Péter (Mosonmagyaróvár, Kossuth L. g. IV. o. t.)

2. Az állítás minden olyan esetben igaz, amikor

A_{1}

B_{1}

C_{1}

és

A_{2}

B_{2}

C_{2}

rendre a

B C

C A

A B

oldalegyenes olyan pontjai, amelyekre egyrészt az

A A_{1}

B B_{1}

C C_{1}

, másrészt az

A A_{2}

B B_{2}

C C_{2}

egyenesek egy

P_{1}

, ill.

P_{2}

ponton mennek át. Ekkor ugyanis a Ceva‐tétel¹ szerint,

X

Y

Z

helyén előbb

A_{1}

B_{1}

C_{1}

-gyel, majd

A_{2}

B_{2}

C_{2}

-vel

\begin{matrix} (A B C_{i}) \cdot (B C A_{i}) \cdot (C A B_{i}) = \frac{A C_{i} \cdot B A_{i} \cdot C B_{i}}{C_{i} B \cdot A_{i} C \cdot B_{i} A} = 1, (i = 1,2) tehát \\ A B_{1} \cdot B C_{1} \cdot C A_{1} = A C_{1} \cdot B A_{1} \cdot C B_{1}, \\ A C_{2} \cdot B A_{2} \cdot C B_{2} = A B_{2} \cdot B C_{2} \cdot C A_{2} . \end{matrix}

Ezeket összeszorozva, majd mindkét oldalt az

α

β

γ

szögek szinuszának feléből képezett szorzattal szorozva az egymás fölötti tényezőhármasok szorzatai rendre éppen az állításbeli területeket adják. ‐ Esetünkben

P_{1}

-nek az

A B C ▵

magasságpontja,

P_{2}

-nek pedig a súlypontja felel meg.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

¹Ha az

A B C ▵

B C

C A

A B

oldalegyenesein rendre

X

Y

Z

olyan a

▵

csúcsaitól különböző pontok, hogy az

A X

B Y

C Z

egyenesek egy pontban találkoznak, akkor

(A B Z) \cdot (B C X) \cdot (C A Y) = + 1

, ahol

(A B Z)

A Z

és

Z B

irányított szakaszok hányadosát, a

Z

osztópontnak az

A

és

B

alappontokra vonatkozó ún. osztóviszonyát jelenti. Lásd pl. Kárteszi Ferenc: A Menelaos és a Ceva‐féle tétel. K. M. L. 11 (1955) 67‐75. o.