Kezdőlap


Feladat:	1067. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Horváth Tibor
Füzet:	1961/november, 109 - 110. oldal		PDF \| MathML
Témakör(ök):	Téglalapok, Síkgeometriai számítások trigonometria nélkül négyszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1960/november: 1067. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $C_{1} C_{2} C_{3} C_{4}$ téglalapban $C_{1} C_{2} = a$ , $C_{1} C_{4} = b$ , és a középpont $K$ , az első felosztás adta téglalapok szélessége $b_{1}$ és $b_{3} = b - b_{1}$ , ezek részeinek hossza a továbbosztás után $a_{1}$ és $a_{2} = a - a_{1}$ , ill. $a_{3}$ és $a_{4} = a - a_{3}$ úgy, hogy a $t_{1} = a_{1} b_{1}$ , $t_{2} = (a - a_{1}) b_{1}$ , $t_{3} = a_{3} b_{3}$ , $t_{4} = (a - a_{3}) b_{3}$ területű rész‐téglalapoknak rendre egy‐egy csúcsa $C_{1}$ , $C_{2}$ , $C_{3}$ , $C_{4}$ . Legyen végül középpontjuk rendre $K_{1}$ , $K_{2}$ , $K_{3}$ , $K_{4}$ , és az első felosztással létrejött $t_{1} + t_{2}$ , ill. $t_{3} + t_{4}$ területű téglalapok középpontja 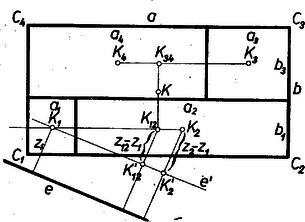$K_{12}$ , $K_{34}$ .

‐ Nyilvánvaló, hogy

K_{1}

K_{12}

és

K_{2}

, valamint

K_{4}

K_{34}

és

K_{3}

egy‐egy a

C_{1} C_{2}

-vel párhuzamos, ettől

b_{1} / 2

, ill.

b - b_{3} / 2

távolságban levő egyenes pontjai, ‐ továbbá hogy

K_{12}

K

és

K_{34}

az eredeti téglalap

C_{1} C_{4}

-gyel párhuzamos középvonalán vannak, vagyis

C_{1} C_{4}

-től

a / 2

távolságban, továbbá

K_{1}

K_{2}

K_{3}

K_{4}

távolsága a

C_{1} C_{4}

oldaltól rendre

a_{1} / 2

a - a_{2} / 2

a - a_{3} / 2

a_{4} / 2

; végül

K

távolsága

C_{1} C_{2}

-től

b / 2

. Ezekkel

K_{1} K_{12} = (a - a_{1}) / 2

és

K_{1} K_{2} = a / 2

.
Legyen

K_{12}

-nek

e

-től mért távolsága

z_{12}

. Feltesszük, hogy

e

K_{1} K_{2}

szakasz

K_{1}

-en túli meghosszabbítását metszi és nem derékszögben. Legyen

K_{12}

és

K_{2}

vetülete a

K_{1}

-en átmenő,

e

-vel párhuzamos

e'

egyenesen

K'_{12}

K'_{2}

. Ekkor a

K_{1} K_{12} K'_{12}

és

K_{1} K_{2} K'_{2}

hasonló derékszögű háromszögekből

K'_{12} K_{12} : K'_{2} K_{2} = K_{1} K_{12} : K_{1} K_{2}

, vagyis

\begin{matrix} (z_{12} - z_{1}) : (z_{2} - z_{1}) = \frac{a - a_{1}}{2} : \frac{a}{2}, és így a_{1} z_{1} + (a - a_{1}) z_{2} = a z_{12} . \end{matrix}

Az egyenlőséget

b_{1}

-gyel szorozva és a

z

távolságok együtthatóiban rendre

t_{1}

t_{2}

és összegük:

t_{1} + t_{2} + t_{12}

kifejezését felismerve

\begin{matrix} t_{1} z_{1} + t_{2} z_{2} = (t_{1} + t_{2}) z_{12} = t_{12} z_{12} . \end{matrix}

(2)

Meggondolásunkat a

K_{3}

K_{4}

és

K_{34}

, valamint a

K_{12}

K_{34}

és

K

középpontú téglalapokra megismételve nyerjük

\begin{matrix} t_{3} z_{3} + t_{4} z_{4} = (t_{3} + t_{4}) z_{34} = t_{34} z_{4}, & (3) \\ t_{12} z_{12} + t_{34} z_{34} = (t_{12} + t_{34}) z = t z . & (4) \end{matrix}

(Ugyanis e két téglalaphármasban az első két téglalap ugyanúgy hézagtalanul és egyrétűen lefedi a 3-ik téglalapot, amint a

K_{1}

és

K_{2}

középpontú téglalapok azt, amelynek középpontja

K_{12}

.) Most már (2) és (3) összeadásával és a jobb oldalon (4) figyelembevételével a bizonyítandó egyenlőséget kapjuk.
(2) ‐ és vele (1) is ‐ akkor is érvényes, ha

e

párhuzamos

K_{1} K_{2}

-vel, vagy merőleges rá. Ugyanis az első esetben

z_{1} = z_{2} = z_{12}

, ezért a

t_{1} + t_{2} = t_{12}

egyenlőséget ezen közös értékkel szorozva kapjuk (2)-t, a másodikban pedig

z_{2} = z_{1} + K_{1} K_{2} = z_{1} + a / 2

, és

z_{12} = z_{1} + K_{1} K_{12} = z_{1} + (a - a_{1}) / 2

, tehát

\begin{matrix} t_{1} z_{1} + t_{2} z_{2} = t_{1} z_{1} + t_{2} z_{1} + \frac{t_{2} a}{2} = (t_{1} + t_{2}) z_{1} + \frac{(a - a_{1}) b_{1} a}{2} = t_{12} z_{1} + \\ + \frac{(a - a_{1}) t_{12}}{2} = t_{12} (z_{1} + \frac{a - a_{1}}{2}) = t_{12} z_{12} . \end{matrix}

e

metszi az eredeti téglalapot, akkor az állítás megjegyzés nélkül nem lehet érvényes, hiszen lehetséges, hogy

e

átmegy

K

-n, de a további középpontok egyikén sem, így pedig (1) bal oldala pozitív, jobb oldala 0, mert

z = 0

. Ellenben valamennyi

z

-nek előjelet tulajdonítva úgy, hogy

e

egyik oldalán levő középpontokra

z > 0

, a másikon levőkre pedig

z < 0

legyen, (1) érvényes marad. Így ugyanis a

z

-knek koordináta jellegük lesz, és a felhasznált

(z_{12} - z_{1}) : (z_{2} - z_{1})

arányra kapott összefüggés érvényes marad, mert a két különbség egyenlő előjelű, hiszen

K_{12}

mindig

K_{1}

és

K_{2}

közé esik. Könnyű belátni végül, hogy előjeles

z

értékekkel (1) a téglalapot metsző és valamelyik oldalával párhuzamos

e

esetén is érvényes.

Horváth Tibor (Szombathely, Nagy Lajos g. IV. o. t.)

Megjegyzés. Számos megoldás koordináta‐geometriai, több más mechanikai meggondolással, egy pedig térmértani segédtétel alapján bizonyította az állítást.