Kezdőlap


Feladat:	1064. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Békési Gábor , Goldperger Katalin , Knuth Előd
Füzet:	1961/október, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Beírt gömb, Egyenes körkúpok, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1960/november: 1064. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a kúp alapsugara $R$ , magassága $m$ , a gömb sugara $r$ . Így a kúp alkotója $\sqrt[]{R^{2} + m^{2}}$ , a henger sugara $r$ , magassága $2 r$ . A kúp tengelymetszete egyenlő szárú háromszög, és a gömbből így kimetszett főkör a háromszög beírt köre, tehát a szokásos jelölésekkel

\begin{matrix} r = \frac{t}{s} = \frac{R m}{R + \sqrt[]{R^{2} + m^{2}}}, innen r \sqrt[]{R^{2} + m^{2}} = R (m - r) és R^{2} = \frac{r^{2} m}{m - 2 r} . \end{matrix}

Így a kérdéses térfogatok

k

aránya:

\begin{matrix} \underset{̲}{k} = V_{1} : V_{2} = \frac{π}{3} R^{2} m : 2 π r^{3} = \frac{r^{2} m^{2}}{3 (m - 2 r)} : 2 r^{3} = \underset{̲}{\frac{m^{2}}{6 m r - 12 r^{2}}} . \end{matrix}

Az aláhúzott részt

r

-re vonatkozó egyenletnek tekintve és megoldva:

\begin{matrix} 12 k r^{2} - 6 k m r + m^{2} = 0, r = \frac{m}{12 k} [3 k \pm \sqrt[]{3 k (3 k - 4)}] . \end{matrix}

(1)

Mivel

k

nyilván pozitív, azért valós megoldás csak

3 k - 4 \geq 0

, azaz

k \geq 4 / 3

esetén van. Tehát

k = 1

lehetetlen,

V_{1} \neq V_{2}

. Ezt kellett bizonyítanunk.
A

k_{min} = 4 / 3

esetben (1)-ből

r = m / 4

, tehát a kúp csúcsának a gömb középpontjától való távolsága

m - r = 3 r

. A kívánt szöget úgy kapjuk, hogy egy tetszés szerinti

r

sugarú körhöz egy a középponttól

3 r

-nyire levő pontból meghúzzuk az érintőket és szögüket megfelezzük.

Békési Gábor (Ócsa, Bolyai J. g. IV. o. t.)

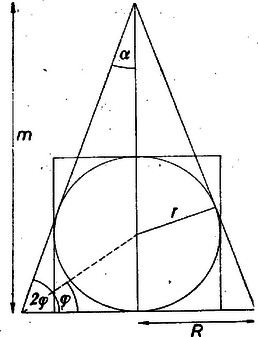II. megoldás. Legyen az alkotók hajlásszöge az alaphoz

2 φ

. Ekkor

m = R tg 2 φ

r = R tg φ

, és így

\begin{matrix} k = \frac{π}{3} R^{3} tg 2 φ : 2 π R^{3} {tg}^{3} φ = \frac{tg 2 φ}{6 {tg}^{3} φ} = \frac{2 tg φ}{6 (1 - {tg}^{2} φ) {tg}^{3} φ} = \frac{1}{3 {tg}^{2} φ (1 - {tg}^{2} φ)} . \end{matrix}

k

-ra akkor kapunk legkisebb értéket, ha itt a nevezőbeli

{tg}^{2} φ (1 - {tg}^{2} φ)

szorzat a legnagyobb. Mivel

2 φ < 90^{\circ}

φ < 45^{\circ}

, azért a második tényező is pozitív. A tényezők összege állandó: 1, tehát a pozitív számok számtani és mértani közepének nagyságviszonyára ismert tétel szerint a szorzat a tényezők egyenlősége esetén a legnagyobb.

{tg}^{2} φ = 1 - {tg}^{2} φ

-ből

tg φ = 1 / \sqrt[]{2}

tg 2 φ = 4 / \sqrt[]{2}

, innen a keresett

α

félnyílásszögre

tg α = \sqrt[]{1 / 8}

sin α = 1 / 3

α

bármelyikből egyszerűen szerkeszthető.

Goldperger Katalin (Balassagyarmat, II. sz. g. IV. o. t.)

Megjegyzések. 1. A gömböt (és vele a hengert is) állandónak véve legyen

r = 1

, ekkor

tg φ = 1 / R

m = R tg 2 φ = 2 R^{2} / (R^{2} - 1)

, és így

\begin{matrix} V_{1} = \frac{2 π R^{4}}{3 (R^{2} - 1)}, amiből R^{2} = \frac{1}{4 π} [3 V_{1} \pm \sqrt[]{3 V_{1} (3 V_{1} - 8 π)}], \end{matrix}

tehát

V_{1} \geq 8 π / 3

V_{min} = 8 π / 3

. Másrészt

V_{2} = 2 π

, tehát

k_{min} = \frac{4}{3}

Knuth Előd (Budapest, I. István g. IV. o. t.)

2. A gömb térfogata

V = 2 V_{2} / 3

, azért a

V_{1} / V = 3 k / 2

arány legkisebb értéke 2. Eszerint a kúpba írt gömb térfogata legfeljebb fele lehet a kúp térfogatának. A fenti szerkesztéssel éppen a maximumot adó félnyílásszöget adtuk meg.