Kezdőlap


Feladat:	1060. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bodó Zoltán , Kiss Sándor , Kóta József , Kucza János , Nagy Péter
Füzet:	1961/október, 60 - 62. oldal		PDF \| MathML
Témakör(ök):	Egyenletrendszerek grafikus megoldása, Másodfokú (és arra visszavezethető) egyenletrendszerek, Feladat
Hivatkozás(ok):	Feladatok: 1960/október: 1060. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. (1) és (2) az $u = x^{2} + y^{2}$ és $v = x y$ új ismeretlenekre nézve elsőfokú egyenletrendszer:

\begin{matrix} 3 u - v = 16, 7 u - 4 v = 38. \end{matrix}

Innen

u = 5, 2

v = - 0, 4

. ‐ Ezekből kiszámíthatjuk

w = x + y

értékét:

u + 2 v = x^{2} + y^{2} + 2 x y = {(x + y)}^{2} = w^{2} = 4, 4

, tehát

w = \pm \sqrt[]{4, 4}

. ‐ Most már

x

és

y

értékét a

\begin{matrix} z^{2} - w z + v = 0 \end{matrix}

egyenlet gyökei adják:

\begin{matrix} z = \frac{1}{2} (w \pm \sqrt[]{w^{2} - 4 v}) = \frac{1}{2} (\pm \sqrt[]{4, 4} \pm \sqrt[]{6}) = \pm \sqrt[]{1, 1} \pm \sqrt[]{1, 5}, \end{matrix}

ahol a két négyzetgyök előtt

\pm

előjel-pár egymástól független. Az előjelek minden párosításával 4 megoldást kapunk: 3

x_{1}

\sqrt[]{1, 1}

\sqrt[]{1, 5}

x_{2}

\sqrt[]{1, 1}

\sqrt[]{1, 5}

x_{3}

\sqrt[]{1, 1}

\sqrt[]{1, 5}

x_{4}

\sqrt[]{1, 1}

\sqrt[]{1, 5}

és így

y = w - x

alapján ‐ itt már azonban

w

-nek az

x

-ben használt előjelével ! ‐

\begin{matrix} y_{1} = + \sqrt[]{1, 1} - \sqrt[]{1, 5} = x_{2}, y_{2} = x_{1}, y_{3} = x_{4}, y_{4} = x_{3} . \end{matrix}

Négy értékes jegyre a négyzetgyöktáblázat alapján

\sqrt[]{1, 1} \approx 1, 049

és

\sqrt[]{1, 5} \approx

\approx 1, 225

, ezért legfeljebb

0, 001

hibával 3

x_{1}

y_{2}

\approx

2,274,

y_{1}

x_{2}

\approx

-0,176

x_{3}

y_{4}

\approx

0,176,

y_{3}

x_{4}

\approx

-2,274.

Kiss Sándor (Szombathely, Nagy Lajos g. IV. o. t.)

II. megoldás. Az I. megoldás alapján kereshetjük mindjárt azt a

λ

μ

számpárt, amellyel (1)

λ

-szorosának és (2)

μ

-szörösének összege egyenlő

x^{2} + y^{2} + 2 x y = {(x + y)}^{2}

-nel, más szóval: amellyel az összegben

x^{2} + y^{2}

együtthatója 1, és

x y

együtthatója 2, vagyis

\begin{matrix} 3 λ + 7 μ = 1 - λ - 4 μ = 2. \end{matrix}

Innen

λ = 3, 6

μ = - 1, 4

. Ekkor

{(x + y)}^{2} = 16 λ + 38 μ = 4, 4

, tehát ismét

x + y = \pm 2 \sqrt[]{1, 1}

. ‐ Hasonlóan kapunk egyenletet

{(x - y)}^{2} = x^{2} + y^{2} - 2 x y

-ra, és ebből

x - y

-ra, azzal a

ν

ξ

számpárral, melyre

\begin{matrix} 3 ν + 7 ξ = 1 - ν - 4 ξ = - 2. \end{matrix}

Innen

ν = - 2

ξ = 1

, ekkor

{(x - y)}^{2} = 16 ν + 38 ξ = 6

, tehát

x - y = \pm \sqrt[]{6} =

= \pm 2 \sqrt[]{1, 5}

.
Most már

x

és

y

-ra a

2 \cdot 2

előjelváltozatnak megfelelően írhatunk fel 4 elsőfokú egyenletrendszert, pl.

x + y = + 2 \sqrt[]{1, 1}

x - y = + 2 \sqrt[]{1, 5}

-ből a fenti

x_{1}

y_{1}

megoldás adódik.

Kucza János (Jászberény, Lehel Vezér g. III. o. t.)

III. megoldás. Grafikus megoldás céljára megvizsgáljuk, hogy milyen görbe lesz az (1) és (2) képe.
Mindkét egyenletben

x

és

y

-t felcserélve ismét az eredeti egyenlethez jutunk. Eszerint ha egy

P (x_{0}, y_{0})

pont rajta van a görbén, akkor

P' (y_{0}, x_{0})

is rajta van, vagyis a görbe a koordinátatengelyek I. és III. negyedbeli

f_{1}

szögfelezőjére tengelyesen tükrös. Hasonlóan a tengelyek II. és IV. negyedbeli

f_{2}

szögfelezője is tükrös tengelye mindkét görbének, mert

x

helyett

- y

-t és

y

helyett

- x

-et írva is önmagába megy át mindkét egyenlet, tehát

P

-vel együtt

f_{2}

-re való

P'' (- y_{0}, - x_{0})

tükörképe is a görbén van.
Tekintsük ezért a görbéket abban a koordinátarendszerben, melynek tengelyei

f_{1}

és

f_{2}

. Az új koordinátákat

x'

y'

-vel jelölve

x

y

helyére

\begin{matrix} x = \frac{1}{\sqrt[]{2}} (x' - y'), y = \frac{1}{\sqrt[]{2}} (x' + y') \end{matrix}

(3)

lép (lásd a gimn. III. o. tankönyv ,,Hiperbola más helyzetben'' c. pontját, de

x

és

x'

, valamint

y

és

y'

cseréjével), és az új egyenletek

\begin{matrix} 2, 5 x'^{2} + 3, 5 y'^{2} = 16, & (1) \\ 5 x'^{2} + 9 y'^{2} = 38. & (2') \end{matrix}

Eszerint mindkét görbe ellipszis a következő féltengelyekkel: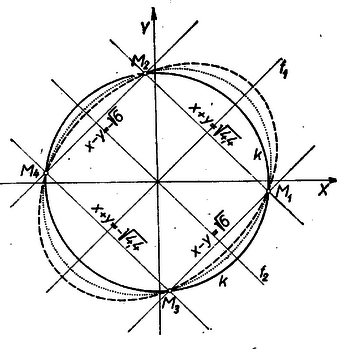

\begin{matrix} a_{1} = \sqrt[]{\frac{16}{2, 5}} \approx 2, 53, b_{1} = \sqrt[]{\frac{16}{3, 5}} \approx 2, 14; a_{2} = \sqrt[]{\frac{38}{5}} \approx 2, 76, b_{2} = \sqrt[]{\frac{38}{9}} \approx 2, 05. \end{matrix}

Látjuk,hogy

a_{2} > a_{1}

és

b_{2} < b_{1}

, tehát a második ellipszis nagytengelyének végpontjai az első ellipszisen kívül vannak, kistengelyének végpontjai viszont annak belsejében, ezért a két ellipszis 4 pontban metszi egymást. Ezeket tudva már az eredeti rendszerben is ábrázolhatjuk (1) és (2)-t az

\begin{matrix} y = \frac{1}{6} (x \pm \sqrt[]{192 - 35 x^{2}}) y = \frac{1}{7} (2 x \pm \sqrt[]{266 - 45 x^{2}}) \end{matrix}

kifejezések alapján is, ‐ ugyanis az (

1'

), (

2'

) alapján való ábrázolás után a leolvasott

x'

y'

megoldásokból

x

y

-t ismét számítanunk kellene (3) alapján.

A metszéspontok 1 tizedes pontossággal

\begin{matrix} M_{1} (2, 3; - 0, 2), M_{2} (- 0, 2; 2, 3), M_{3} (0, 2; - 2, 3) és M_{4} (- 2, 3; 0, 2) . \end{matrix}

Bodó Zoltán (Eger, Dobó I. g. III. o. t.)

Megjegyzések. 1. Az (1) és (2)-t ábrázoló görbék metszéspontjait úgy is megkaphatjuk, mint az egyenletrendszer átalakításával kapott újabb egyenleteket ábrázoló görbék metszéspontjait. Az ellipsziseknél sokkal könnyebben megrajzolható az I. megoldásbeli

x^{2} + y^{2} = 5, 2

kör és az

x + y = \pm \sqrt[]{4, 4}

egyenespár (felhasználva Pythagorász tételét és hogy

\begin{matrix} 5, 2 = 2, 2^{2} + 0, 6^{2} = 1, 8^{2} + 1, 4^{2}, ill. 4, 4 = 2^{2} + 0, 6^{2} + 0, 2^{2} = 1, 8^{2} + 1^{2} + 0, 4^{2}), \end{matrix}

továbbá a II. megoldásbeli

x - y = \pm \sqrt[]{6}

egyenespár

(6 = 2^{2} + 1^{2} + 1^{2})

. A 4 metszéspontot vagy a kör és az egyik egyenespár adhatja, vagy pedig a két egyenespár.

Nagy Péter (Szombathely, Nagy Lajos g. IV. o. t.)

2. A számító megoldást előkészíthetjük az

y / x = q

hányados kiszámításával is, ha (1) és (2)-ből előbb az állandó tagokat küszöböljük ki. (1) és (2)-t

19

-cel, ill.

- 8

-cal szorozva és összeadva

x^{2} + 13 x y + y^{2} = 0

, és innen

q = - 6, 5 \pm

\pm \sqrt[]{41, 25}

. Most már pl.

y = q x

helyettesítéssel (1)-ből

(3 - q + 3 q^{2}) x^{2} = 16

, és átalakításokkal

x = \pm \sqrt[]{2, 6 \pm \sqrt[]{6, 6}}

. ‐ Ennek grafikus megfelelője az, hogy egyik görbe gyanánt az

y = q_{1} x

y = q_{2} x

egyenespárt vesszük. (E két egyenes metszése, az origó, természetesen nem megoldása az (1), (2) rendszernek hiszen ez az egyenespár csak a rendszer egyik másodfokú egyenletét helyettesíti.)

Kóta József (Tatabánya, Árpád g. III. o. t.)