Kezdőlap


Feladat:	1058. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Benczúr A. , Bollobás B. , Farkas Z. , Frint G. , Gagyi Pálffy A. , Glattfelder Péter , Horváth T. , Huber T. , Jójárt I. , Kéry G. , Knuth E. , Kóta G. , Kóta J. , Krámli A. , Kunszt Z. , Lehel J. , Magyar G. , Máté A. , Máté E. , Mócsi Z. , Molnár E. , Nagy Cs. , Náray-Szabó G. , Páska Cs. , Pór A. , Sonnevend Gy. , Szegő K. , Székely J. , Szepesvári I. , Szőts M. , Zalán P.
Füzet:	1961/október, 57 - 59. oldal		PDF \| MathML
Témakör(ök):	Térgeometria alapjai, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1960/október: 1058. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.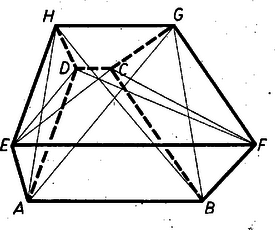

Alkalmazzuk az 1054. feladatban bebizonyított tételt¹ rendre az

A B G H

C D E F

A D H E

B C G F

négyszögre:

\begin{matrix} A G^{2} + B H^{2} = A H^{2} + B G^{2} + 2 A B \cdot H G, \\ C E^{2} + D F^{2} = C F^{2} + D E^{2} + 2 D C \cdot E F, \\ A H^{2} + D E^{2} = A E^{2} + D H^{2} + 2 A D \cdot E H, \\ B G^{2} + C F^{2} = B F^{2} + C G^{2} + 2 B C \cdot F G . \end{matrix}

E négy egyenlőség összegéből a mindkét oldalon szereplő tagokat elhagyva a kívánt egyenlőség adódik.
Ha bármely két testátló metszi egymást, akkor a 471. gyakorlat² szerint egy

M

ponton mennek át, hiszen nem lehetnek egy síkban.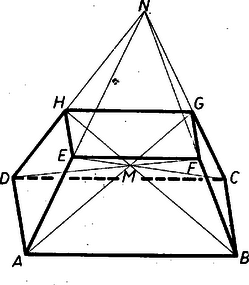

Így az

A G

D F

átlók végpontjai egy síkban vannak. Ez a sík az

A B C D

és

E F G H

lapoknak a feltevések folytán párhuzamos síkjait párhuzamos egyenesekben metszi, ezért

A D | | F G

. Így

E H

A D

F G

és

B C

párhuzamosak, ennélfogva

A B C D

és

E F G H

paralelogrammák. Ekkor

A B \cdot H G = D C \cdot E F

A D \cdot E H = B C \cdot F G

, és a tétel így egyszerűsödik:

\begin{matrix} A G^{2} + B H^{2} + C E^{2} + D F^{2} = A E^{2} + B F^{2} + C G^{2} + D H^{2} + 4 A B \cdot H G + 4 A D \cdot E H . \end{matrix}

Ebben az esetben a test paralelogramma alapú csonka gúla, vagyis az

A E

B F

C G

D H

élek egy

N

ponton mennek át. Ugyanis az

A D F G

trapéz

A D

és

F G

oldalainak aránya, vagy ami ugyanaz, az

A D : E H

arány egyenlő

A M : M G

-vel, folytatólag

M

-nek

A D

és

F G

-től mért, és tovább az

A B C D

és

E F G H

síktól mért távolságainak

m_{1} : m_{2}

arányával. Ugyanígy

A B : E F = A B : H G = m_{1} : m_{2}

, mert az

A G

és

B H

átlók metszéspontja ugyancsak

M

. Már most az

A B F E

(konvex) trapéz

A E

és

B F

szárai

N

metszéspontjának az

A B

E F

oldalaktól mért távolságai arányának, és így az

A N : E N

-nek értéke ugyancsak

m_{1} : m_{2}

, és ez áll a

D C G H

A D E H

trapézokra is. Ezzel állításunkat bebizonyítottuk. (

m_{1} = m_{2}

esetén

N

nem létezik, ekkor a test paralelepipedon.) Ekkor az

A C G E

és

B D H F

trapézek alapján az állítás következő módosulását is kimondhatjuk:

\begin{matrix} A G^{2} + B H^{2} + C E^{2} + D F^{2} = A E^{2} + B F^{2} + C G^{2} + D H^{2} + 2 A C \cdot E G + 2 B D \cdot F H . \end{matrix}

Glattfelder Péter (Pannonhalma, Bencés g. IV o.t.)

Megjegyzés. Azt, hogy a testátlók közös

M

pontja létezése esetén a test csonka gúla, a következőkből is sejthetjük. Az

A D : E H = m_{1} : m_{2} = A B : E F

aránypárból és a

B A D

F G H

szögek térbeli váltószög voltából következik, hogy az

A B C D

és

G H E F

paralelogrammák hasonló helyzetűek, és hasonlósági pontjuk

M

. Kézenfekvőnek látszik tehát, hogy a

G

H

E

F

csúcsok helyére

E

F

G

H

-t írva ugyancsak létezik hasonlósági pont, és ez

N

¹Lásd K. M. L. 23 (1961) 17. o. Ha a

P Q R S

konvex négyszögben

P Q | | R S

, akkor

P R^{2} + Q S^{2} = Q R^{2} + S P^{2} + 2 \cdot P Q \cdot R S

²Lásd K. M. L. 17 (1958) 57. o. Ha a tér $n$ egyenese közül bármelyik kettő metszi egymást, akkor vagy egy síkban vannak, vagy egy ponton mennek át.