Feladat: 1057. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Benczúr A. ,  Bollobás B. ,  Cserháti M. ,  Fritz J. ,  Gagyi Pálffy A. ,  Gálfi l. ,  Grüner Gy. ,  Juhász István ,  Kiss Ildikó ,  Lehel J. ,  Nagy Csaba ,  Nováky B. ,  Opálény M. ,  Páska Cs. ,  Paulik L. ,  Sári P. ,  Sebestyén Z. ,  Székely J. ,  Szoboszlai L. ,  Tardos Csilla 
Füzet: 1961/október, 56 - 57. oldal  PDF  |  MathML 
Témakör(ök): Kocka, Mértani helyek, Feladat
Hivatkozás(ok):Feladatok: 1960/október: 1057. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Legyen az XY szakasz P felezőpontjának az ABCD=L, ill. a vele párhuzamos A'B'C'D'=L' lapon levő vetülete 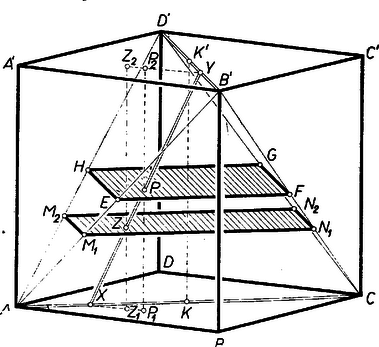P1, ill. P2.

 
 

A PP1X és PP2Y derékszögű háromszögek egybevágók, mert P-nél levő szögeik csúcsszögek, és átfogóik egyenlők, ezért PP1=PP2, vagyis P mindig egyenlő távolságra van L és L'-től. Ugyanezt jelenti a PX=PY egyenlőség arra az esetre, ha X az AC átló K és Y a B'D' átló K' felezőpontjában van, mert ekkor XY≡KK', merőleges L-re (ekkor az említett háromszögek elfajulnak). Ezek szerint a keresett mértani hely a kockának az AA' élre merőleges S szimmetriasíkjában van.
Ha X-et rögzítjük és Y végigfut B'D'-n, akkor P leírja az XB'D' háromszög B'D'-vel párhuzamos középvonalát, melynek hossza B'D'/2. E szakasz szimmetrikus az ACC'A' síkra és a kocka középpontjától való távolsága XK/2. Ha X végighalad AC-n, ez a szakasz a saját irányára merőlegesen tolódik el, mert AC merőleges B'D'-re; az eltolódás hossza, míg XA-tól K-ig, majd C-ig halad, AK/2+KC/2=AC/2=B'D'/2. Tehát a szakasz által leírt idom az EFGH=Q négyzet, ahol E és H az X≡A, F és G pedig az X≡C helyzethez tartozó végpontjai a szakasznak, az AB', AD', CB', CD' lapbeli átlók felezőpontjai, a kocka oldallapjainak középpontjai. Eszerint P csak a Q négyzet belsejében vagy kerületén lehet.
Fordítva, ha P a Q-nak egy tetszés szerinti pontja, akkor található AC-n olyan X és B'D'-n olyan Y, hogy XY felezőpontja éppen P, éspedig X-et a PB'D' sík, Y-t a PAC sík metszi ki. Valóban, P, X, Y mindegyike benne van mindkét síkban, tehát egy egyenesben, a két sík metszésvonalán vannak, és P felezi az XY szakaszt, mert X, P, Y rendre az L, S, L' sík pontja.
Ezek szerint az XY szakaszok felezőpontjának mértani helye a Q négyzet területének minden (belső és kerületi) pontja.
Eredményünket szemléletesen így is kimondhatjuk: az XY szakasz mindig az ACB'D'=T (szabályos) tetraéder belsejében, vagy valamelyik lapján, vagy élén van, a keresett mértani hely pedig T-nek az S síkkal való metszete.
b) Hasonlóan adhatjuk meg a Z pontok mértani helyét. Ha Z vetülete L és L'-re Z1, Z2, akkora ZZ1X és ZZ2Y derékszögű háromszögek hasonlók; átfogóik aránya 1:2, ezért Z-re az L és L'-től mért távolságok aránya mindig 1:2, a mértani hely abban az L-lel párhuzamos S* síkban van, amely az AA' oldalélt 1:2 arányban osztja. Kézenfekvő az a sejtés, hogy Z mértani helye a T-nek S*-gal való metszete. Ennek a fentiekhez hasonló bizonyítását mellőzve csak az eredményt mondjuk ki. Az AB', CB', CD', AD' átlókat 1:2 arányban osztó pontokat M1, N1, N2, M2-vel jelölve Z mértani helye az M1N1N2M2 téglalap minden belső és kerületi pontja. A téglalap oldalai: M1M2=B'D'/3 és M1N1=2AC/3.
 

Juhász István (Budapest, Madách I. g. IV. o. t.)
 

Megjegyzések. 1. P mértani helyét a következő könnyen bizonyítható segédtétel alapján is megkaphatjuk: Ha egy XY szakaszt és P felezőpontját (párhuzamos vetítéssel) valamely S síkra vetítünk, akkor P-nek P' vetülete felezi a szakasz X'Y' vetületét. ‐ Összes XY szakaszainkat a fenti S-re vetítve csak azt kell belátnunk, hogy ha X' az A''C'' és Y' a B''D'' átló valamely pontja, akkor P' amely itt azonos P-vel ‐, az EFGH négyzet belsejében vagy a kerületén van.
2. A segédtétel alapján az I. megoldástól függetlenül úgy is kereshetjük a mértani helyet, hogy XY szakaszainkat egyrészt L-re, másrészt a kocka valamelyik oldallapjára vetítjük. Az utóbbi esetben a vetület az oldallap L-lel párhuzamos oldalfelezője.
3. A legtöbb versenyző csak azt mutatta meg, hogy P nem fekhet kívül Q-n, de nem bizonyította be, hogy Q minden pontja valamely XY szakasznak felezőpontja.