| Feladat: | 1054. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bónis Katalin , Kéry Gerzson , Kunszt Zoltán , Lázár Zsolt , Molnár Emil , Nagy Irén , Nagypál Botond | ||
| Füzet: | 1961/szeptember, 17 - 19. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Négyszögek geometriája, Síkgeometriai számítások trigonometria nélkül négyszögekben, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1960/szeptember: 1054. matematika feladat | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.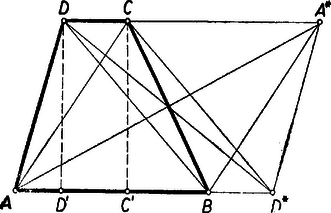 I. megoldás: és párhuzamossága folytán az négyszög trapéz. Legyen a , csúcs vetülete -n , , így az , , és derékszögű háromszögekből Pythagorász tételével és azt kell megmutatnunk, hogy itt a jobb oldal egyenlő -vel. Feltehetjük, hogy az -nál levő szög nem nagyobb derékszögnél, így a konvexség miatt az egyenesen , , egymás után következő pontok: . Ezért (2) jobb oldalának első különbsége A második különbség , és kölcsönös helyzete szerint háromféleképpen alakulhat:
Megjegyzések. 1. Elkerülhetjük az esetek szétválasztását, ha az átlók négyzetét a trapéz 4 rész‐háromszögéből a koszinusz‐tétellel fejezzük ki, figyelembe véve, hogy és : , amiből a 0-tól különböző -vel osztva (1)-re jutunk. ‐ Az esetek szétválasztását az tette elkerülhetővé, hogy a koszinusz‐tételről annak idején megmutattuk, hogy hegyes-, tompa- és derékszögű háromszögre egyaránt érvényes.
2. Lényegében ugyanígy kerülhetjük el az esetszétválasztást, ha ábránkra koordinátarendszert helyezünk, és a kifejezéseket a csúcsok koordinátáival állítjuk elő.
3. Az állítás a húrnégyszögre vonatkozó Ptolemaiosz‐tétel felhasználásával is bizonyítható.
II. megoldás. Az I. megoldás jelöléseit tovább használva tükrözzük az trapézt a oldal felezőpontjára, legyen és képe , , és alkalmazzuk az 1006. feladat1 első tételét az , és paralelogrammákra: Mármost (8) és (9) összegéből (10)-et kivonva rendezés és egyszerűsítés után (1)-et kapjuk.
III. megoldás. Az állítást vektoralgebrai úton bizonyítjuk. Ha már most , és a trapéz nem hurkolt, vagyis és egyirányúak, akkor
Megjegyzés. A bebizonyított tétel és az 1006. feladat segédtétele felhasználásával kifejezhetjük a trapéz alapú hasáb testátlóinak négyzetösszegét az éleivel. 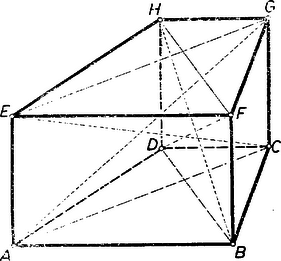 Ha az trapéz alapú hasáb oldalélei , , , , akkor a testátlók négyzetösszege, mint az és paralelogrammák átlóinak négyzetösszege:
1Lásd a megoldást K. M. L. 21 (1960) 20. o. |