Kezdőlap


Feladat:	1052. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Benczúr A. , Bollobás B. , Farkas Z. , Frint Gábor , Gálfi l. , Gallyas Györgyi , Glattfelder Péter , Hegedüs I. , Horváth T. , Kéry G. , Knuth E. , Nagy Csaba , Nagy Dezső , Nagypál B. , Nováky B. , Opálény M. , Sebestyén Z. , Simonovits M. , Szegi A.
Füzet:	1961/szeptember, 13 - 16. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Magasságpont, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1960/szeptember: 1052. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az $A' A''$ összekötő egyenes megadja a $B C = a$ oldalegyenest. Az $A A'$ belső és $A A''$ külső szögfelezők merőlegesek egymásra, ezért $A$ az $A' A''$ szakasz fölé írt $ϰ$ Thalész‐körön van. Másrészt $A M = m$ merőleges $B C$ -re, tehát $A$ -t $ϰ$ és $m$ metszéspontja tűzi ki. Legyen $m$ és $a$ metszéspontja 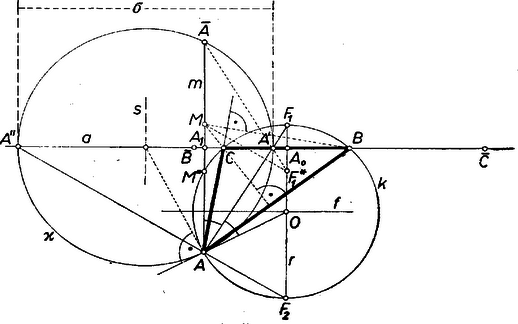$A_{1}$ .
Ismeretes, hogy $M$ -nek $A_{1}$ -re való $M^{*}$ tükörképe rajta van a háromszög $k$ körülírt körén, ezért $k$ -nak $O$ középpontja az $A M^{*}$ szakasz felező merőlegesén fekszik. Másrészt $A A'$ felezi az $O A A_{1}$ szöget,¹ ezért $O$ rajta van $A A_{1}$ -nek $A A'$ -re való tükörképén. Ezekből $O$ megszerkeszthető. Végül az $O$ körül $O A$ sugárral írt $k$ kör $a$ -ból kimetszi a $B$ , $C$ csúcsokat.

1. ábra

Nem kapunk

A

pontot, ha

M

kívül van azon a

σ

síksávon, amelyet az

A'

és

A''

-ben

A' A''

-re állított merőlegesek határolnak. Akkor sincs megoldás, ha

M

σ

-nak egyik határegyenesén van, mert így

A

B C

egyenesre esnék.

σ

belsejében levő

M

-mel

A

-ra 2 helyzet adódik

a

két oldalán:

A

és

\bar{A}

. ‐

M^{*}

egyértelműen szerkeszthető.

A A_{1}

fenti tükörképe akkor és csak akkor nem tűzi ki

O

-t, ha párhuzamos

f

-fel, és így

a

-val is. Ilyenkor

A_{1} A A' ∢ = 45^{\circ}

, és

A

(tehát

M

is)

σ

-nak

s

felezővonalán van, vagyis

M A' = M A''

. ‐ Ha

M A' < M A''

, akkor nyilván

O A' < O A''

, viszont

M A' > M A''

esetén

A'

és

A''

szerepe felcserélődik.

k

akkor és csak akkor metszi

a

-t, ha

O

-nak

a

-tól való távolsága kisebb

O A

-nál.

A

-nak arra a helyzetére, amely

a

-nak

M

-et tartalmazó pontján van, mindig kapunk megoldást, mert így

A M^{*} > A A_{1}

(és ebben

B

és

C

-nél hegyesszög van.)
Ha

M

a

-n van, akkor a háromszög derékszögű, a 2 megoldás egymás tükörképe. (Mindkettő megoldásnak tekintendő, mert kizárólag helyzetadatokból szerkesztünk, tehát az

A B C

háromszög csúcsainak is a lehetséges helyzeteit keressük.) Akkor is derékszögű háromszög a megoldás, ha

M

ϰ

körön van (s így

A

egyik helyzete

M

-be esik); ilyenkor a másik megoldás elfajul.

Gallyas Györgyi (Budapest, Szilágyi Erzsébet lg. IV. o. t.)

Megjegyzések. 1. Legyenek

F_{1}

, és

F_{2}

B C

oldal felező merőlegesének

k

-n levő pontjai, a két

B C

ív felezőpontjai. Az

A O

egyenest abból is megkaphatjuk, hogy az

A F_{1} F_{2}

háromszög súlyvonala

A O

. Mivel

F_{1}

A A'

-n,

F_{2}

pedig az

A A''

-nek

A

-n túli meghosszabbításán van, azért az

A O

egyenest bármely az

A F_{1} F_{2}

-höz hasonló helyzetű háromszög súlyvonalából megkaphatjuk: ha egy az

A' A''

-re merőleges tetszés szerinti egyenes

A A'

-t,

A A''

-t

G_{1}

G_{2}

-ben metszi, és

G_{1} G_{2}

felezőpontja

G

, akkor

A O \equiv A G

.
2. Továbbmenve

A O

-t mint

ϰ

-nak

A

-beli érintőjét is megkaphatjuk. Ha ugyanis valamely az

R

-nél derékszögű

P Q R

háromszög

P R

Q R

befogójának felezőpontja

Q_{0}

P_{0}

, és

R

vetülete

P Q

-ra

R_{1}

(2. ábra), akkor

R

és

R_{1}

P_{0}

Q_{0}

-ra tükrösek, ennélfogva a

P R R_{1}

és

O R R_{1}

, háromszögek

R_{1}

-ből kiinduló súlyvonalai egymásra merőlegesek.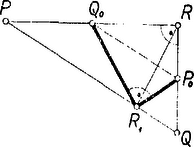

2. ábra

3. Sok dolgozat a megoldások számát legfeljebb 1-ben állapította meg, mert

A

-nak csak egyik helyzetét vette tekintetbe. Ezt vagy azzal a szűk szemlélettel lehet megmagyarázni, hogy

M

-nek a háromszög belsejében ,,kell'' lennie, másképpen, hogy a háromszög csak hegyesszögű lehet ‐, vagy annak az elvnek téves értelmezésével, hogy szimmetrikus megoldások egyikét mellőzni szoktuk.

A

és

\bar{A}

valóban szimmetrikus

A' A''

-re, viszont

M

általában az egyik félsíkon van, tehát a két félsík nem egyenértékű. ‐ Az efféle nézetek némi ellensúlyozása végett ábránkon a szétválasztott

A

és

M

esetét részleteztük, a másik megoldásnak csak

\bar{A}

\bar{B}

\bar{C}

csúcsait tüntettük fel.
A következő két megoldás

A

-nak a fentiek szerinti ismeretére támaszkodva más úton fejezi be a szerkesztést.

II. megoldás: Megszerkesztjük a

B C

oldal

A_{0}

felezőpontját. Legyen az

A M

átmérő fölötti

k_{1}

kör középpontja

K

(3. ábra), továbbá

A B

-vel,

A C

-vel és

A A'

-vel való metszéspontja rendre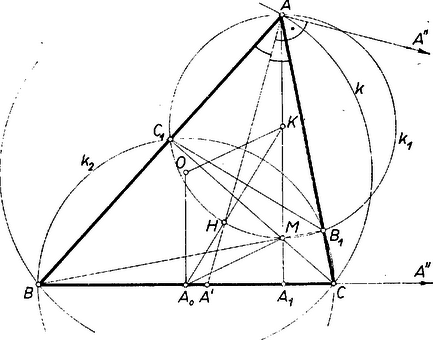

C_{1}

B_{1}

H

3. ábra

Így

M C_{1} A ∢ = M B_{1} A ∢ = 90^{\circ}

, tehát

C_{1}

és

B_{1}

C

, ill.

B

-ből húzott magasság talppontja.

A H

felezi a

B A C = C_{1} A B_{1}

szöget, ezért

H

felezi az egyik

C_{1} B_{1}

ívet, ennélfogva a

B_{1} C_{1}

szakasz felező merőlegese

K H

. Másrészt

B_{1}

és

C_{1}

B C

átmérő fölötti vagyis

A_{0}

középpontú

k_{2}

Thalész-körnek pontjai, ezért

B_{1} C_{1}

felező merőlegese átmegy

A_{0}

-on. Ezek szerint

K H

és

a

metszéspontja

A_{0}

.
Most már

O

-t abból kapjuk, hogy irány és nagyság szerint

A_{0} O = M A / 2 = M K = K A

, ennélfogva

O

A_{0} M K O

(vagy

A_{0} K A O

) paralelogramma negyedik csúcsa.

Nagy Csaba (Budapest, József A. g. IV. o. t.)

Megjegyzés.

A_{0}

ismeretében

O

-t megkaphatjuk az Euler‐egyenesen fekvő nevezetes pontok közti távolságviszonyok alapján is:

A_{0} A

-nak

A_{0}

-hoz közelebbi harmadoló pontja az

S

súlypont, és

M S

A_{0}

-ban

a

-ra állított merőlegest

O

-ban metszi.

Glattfelder Péter (Pannonhalma, Bencés g. IV. o. t.)

III. megoldás: Az

A_{0} O = M A / 2

összefüggés és némi számítás alapján megszerkeszthetjük

F_{1}

-nek

a

-ra való

F_{1}^{*}

tükörképét (1. ábra), majd az ezen át

a

-ra állított merőlegessel az I. megoldás

f

egyeneséből kimetszhetjük

O

-t.

k

sugarát

r

-rel jelölve

\begin{matrix} F_{2} F_{1}^{*} = F_{2} A_{0} - F_{1}^{*} A_{0} = F_{2} A_{0} - A_{0} F_{1} = \\ = (r + O A_{0}) - (r - O A_{0}) = 2 O A_{0} = A M, \end{matrix}

így

F_{2} A M F_{1}^{*}

paralelogramma, tehát

F_{1}^{*} M

párhuzamos

F_{2} A \equiv A A''

-vel. Másrészt

F_{1}^{*}

, mint

A A''

tükörképének pontja, rajta van az

A A'

egyenesen, tehát megszerkeszthető. (Hasonlóan metszhetjük ki

F_{2}

tükörképét az

M

-en át

A A'

-vel húzott párhuzamosból az

\bar{A} A''

egyenessel.)

Megjegyzés. Több számolás alapján az

A_{0} A_{1}

szakaszt negyedik arányosként megszerkeszthetjük és

A_{0}

-t így is kitűzhetjük.

Frint Gábor (Mosonmagyaróvár, Kossuth L. g. III. o. t.)

¹L. pl. az 598. gyakorlatot K. M. L. 21 (1960) 23. o.