Feladat: 1051. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bácsy Zs. ,  Benczúr András ,  Bodó Z. ,  Bollobás Béla ,  Dömötör Gy. ,  Fritz J. ,  Gálfi László ,  Juhász István ,  Kéry G. ,  Knuth Előd ,  Kovács I. ,  Krámli András ,  Kunszt Z. ,  Máté A. ,  Molnár Emil ,  Nováky Béla ,  Opálény M. ,  Simonovits Miklós ,  Szarka Gy. ,  Vesztergombi György ,  Zalán P. 
Füzet: 1962/január, 17 - 20. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1960/szeptember: 1051. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Tekintsük először a metszéspontok számának kérdését.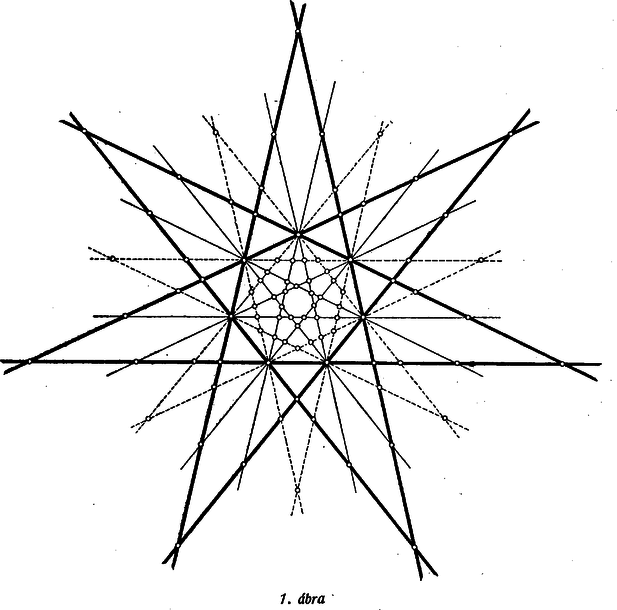
a) A H hétszög mindegyik oldalegyenesét a többi 6 oldalegyenes mindegyike metszi (1. ábra, vastag), mert nincsenek köztük párhuzamosak, éspedig mindegyik más pontban. Ugyanis H konvex, mindegyik oldalegyenesének az egyik partján fekszik, ezért a bármelyik két oldalegyenes által létrejött 4 szögtartomány közül csak egyben van pontja úgy, hogy ennek mindegyik szárán van csúcsa. Ha a szögtartomány csúcsán egy harmadik oldalegyenes is átmenne, ez kettévágná H-t, ami lehetetlen. ‐ A metszéspontok összes száma 7⋅6/2=21, mert a 7⋅6 szorzatban minden metszéspontot 2-szer veszünk számba.

 
 

b) Kétféle átló van. Az egyik féle egy csúcsból a rá következő 2-ik csúcshoz vezet, merőleges a közbülső csúcson átmenő szimmetriatengelyre, és így párhuzamos az ezen csúccsal szemben fekvő oldallal (az ábrán szaggatva). A másik féle átló a kiindulási csúcsot a rá következő 3-ik csúccsal köti össze, párhuzamos a közbülső 2 csúcsot összekötő oldallal. Mindkét féle átlóból 7 van. A párhuzamosságok folytán a 14 átló- és 7 oldalegyenes 3-asával 7 irányt képvisel, bármelyik két irány közti szög a 180∘/7=ε szögnek egész számú többszöröse.
Mármost a 14 átló mindegyikét 12 másik metszi, éspedig 3 ‐ 3 átló 1 ‐ 1 csúcspontban, mert H minden csúcsán 4 átló megy át, a többi 6 külön-külön. Eszerint 14⋅6/2=42 metszésponton 2 ‐ 2 átlóegyenes megy át, a 7 csúcsot hozzájuk véve az átlóegyenesek különböző metszéspontjainak száma 49.
c) A 21 oldal- és átlóegyenes mindegyikét 18 másik metszi, éspedig 5 ‐ 5 az illető egyenesen levő 2 csúcsban, mert H minden csúcsán 6 egyenes megy át, a többi 18-2⋅5=8 külön-külön. Eszerint 21⋅8/2=84 metszésponton 2 ‐ 2 egyenes megy át, és a különböző metszéspontok száma 84+7=91.
 
II. a) Három egyenes csak akkor nem határoz meg háromszöget, ha egy ponton mennek át, vagy ha van köztük párhuzamos. Az oldalegyenesek rendszerében ez egyetlen egyeneshármasra sem teljesül, bármely kiválasztott 3 oldalegyenes háromszöget ad. A háromszög oldalegyeneseinek megválasztásában lépésről lépésre haladva az a oldalegyenest H oldalegyenesei közül 7-féleképpen választhatjuk, b-t a fennmaradtakból 6, végül c-t 5-féleképpen. Az így adódó 7⋅6⋅5=210 megválasztásban azonban minden háromszöget annyiszor veszünk tekintetbe, ahányféleképpen egymás utáni oldalegyeneseit megbetűzhetjük, vagyis 6-féleképpen:
a,b,c;a,c,b;b,a,c;b,c,a;c,a,b;c,b,a.
Eszerint a különböző háromszögek száma 210:6=35.
b) Az előző meggondolás mintájára az átlóegyenesek közül a-t 14-, b-t pedig 14-2=12-féleképpen választhatjuk (mert az a-nak vett átlóval párhuzamos átlóval nem kapnánk háromszöget). Ha a és b nem H valamely csúcsában metszik egymást ‐ a 14⋅12 lehetőségből I. b) szerint 14⋅6 esetben ‐, akkor c gyanánt a hátralevő 14-2⋅2=10 más irányú átló mindegyike vehető. A további 14⋅6 esetben a és b metszéspontján még 2 átló megy át, ezért c választására csak 10-2=8 lehetőség marad. Az így számba vett 14⋅6⋅10+14⋅6⋅8=1512 háromszög ismét 6-onként csak oldalainak sorrendjében különböző, így a különbözők száma 252.
c) Mind a 21 egyenes közül a és b 21⋅18-féleképpen választható. Metszéspontjuk I. c) szerint 21⋅8 esetben nem csúcsa H-nak és 21⋅10 esetben csúcsa; ezért c gyanánt 21-2⋅3=15, ill. 15-(6-2)=11 egyenes választható, és a különböző háromszögek száma (21⋅8⋅15+21⋅10⋅11)/6=805.
III. Az egyenlő szárú háromszögek hasonló megszámlálása céljára megjegyezzük, hogy mivel szögeik ε többszörösei, és összegük 180∘=7ε, azért a főcsúcsukban levő szög ε-nak páratlan számú többszöröse. Így bármely két egyenesünk metszéspontja szerepelhet egyenlő szárú háromszög főcsúcsa gyanánt, mert az általuk bezárt 2-féle szög egyike páratlan többszöröse ε-nak, hiszen összegük páratlan többszöröse neki. Ha a két szár egyenesét megválasztottuk, akkor a köztük levő 2kε alakú szög (a főcsúcsnál levő külső szög) felezője kijelöli az alap egyenesének irányát.
a) Az oldalegyenesek rendszeréből a két szárt a fentiekhez hasonlóan 7⋅6/2=21-féleképpen választhatjuk meg. Mivel minden metszésponton csak 2 oldalegyenes megy át, azért a szárakhoz a fentiek szerint meghatározott alap-irányt képviselő egyetlen egyenes nem megy át a szárak metszéspontján, így minden esetben 1 egyenlő szárú háromszöget kapunk. Összes számuk 21, éppen annyi, mint az oldalegyenesek metszéspontjainak száma. Valóban, az előzők szerint az oldalegyenesek minden metszéspontja 1 egyenlő szárú háromszögben szerepel főcsúcs gyanánt.
b) Az átlóegyenesek 42 olyan metszéspontját véve főcsúcs gyanánt, amelyen csak 2 egyenes megy át ‐ amely tehát nem csúcsa H-nak, ‐ minden esetben 2 egyenlő szárú háromszöget kapunk, mert a fentiek szerint meghatározott alapiránnyal 2 átló párhuzamos.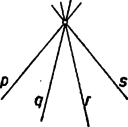
 
 
2. ábra
 

Ha pedig H valamely csúcsát vesszük főcsúcsnak, a rajta átmenő 4 átlóegyenes közül a 2 szárat 4⋅3/2=6-féleképpen választhatjuk. Ezek közül 2 esetben a köztük levő 2kε alakú szög felezője ugyancsak átlóegyenes, ugyanis a 2. ábrán q felezi az r és p közti szöget, és r az s és q közöttit; a többi 4 esetben ez nem áll fenn. E 4 esetben a 2 szár ugyancsak 2 átlóval alkot egyenlő szárú háromszöget. A 2 kiemelt esetben viszont 1 ‐ 1 háromszög elmarad. Így H mindegyik csúcsa 4⋅2+2⋅1=10 egyenlő szárú háromszögnek főcsúcsa. Az átlóegyenesekkel meghatározott egyenlő szárú háromszögek összes száma 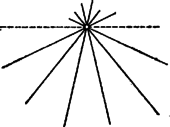42⋅2+7⋅10=154.
 
 
3. ábra
 

c) Hasonlóan az átló és oldalegyeneseknek mind a 84 olyan metszéspontja, melyen csak 2 egyenes megy át, 3 egyenlő szárú háromszögnek főcsúcsa, mert a szárakkal meghatározott alap-iránnyal 3 egyenes párhuzamos. A H bármelyik csúcsán átmenő 6 egyenes közül (3. ábra) a szárak 6⋅5/2=15-féleképpen választhatók. Az alap iránya majdnem minden esetben az illető csúcson átmenő egyenesek között is szerepel, csak abban a 3 esetben nem, amelyben a 2 szár az illető csúcsban hiányzó egyetlen irányra tükrös. Ebben a 3 esetben a 2 szár 3-féleképpen egészíthető ki egyenlő szárú háromszöggé, a többi 12 esetben csak 2-féleképpen. Mindezek szerint az átló- és oldalegyenesekkel meghatározott háromszögek közül az egyenlő szárúak száma: 84⋅3+7(3⋅3+12⋅2)=483.
IV. A 7 második féle átló H belsejében egy kisebb H1 szabályos hétszöget határol (1. ábra), ezen az első féle átlók nem mennek át, mert a középponttól távolabb vannak, mint a második féle átlók. H1 mindegyik oldalához 1 ‐ 1 egyenlő szárú háromszög csatlakozik, ezek szomszédos párjai közé 1 ‐ 1 szimmetrikus ötszög (összesen 7), majd ezek közé 1 ‐ 1 deltoid illeszkedik, így az első féle átlókkal határolt H2 szabályos hétszög területén 1+3⋅7=22 idom van. Egy első féle átlón kívül 5 háromszög van (a lemetszett csúcsból kiinduló 6 egyenes között); a szélsők azonban a szomszédos első féle átlókhoz is hozzátartoznak, így a H és H2 közötti idomok száma 7⋅5-7=28. Az összes idomok száma 22+28=50.
Knuth Előd (Budapest, I. István g. IV. o. t.)

 
Megjegyzések. 1. A megszámlálásokra több más lehetőség is van. Pl. a II. b) és c) részben a háromszög oldalegyeneseinek irányát ‐ a II. a) rész szerint ‐ 35-féleképpen választhatjuk, ez után a helyzetüket 2 ‐ 2, ill. 3 ‐ 3-féleképpen, ezért 35⋅23, ill. 35⋅33 lehetőségre gondolunk. Így azonban egy ponton átmenő egyeneshármasokat is számításba vettünk. Ezek közös pontja mindig egy hétszögcsúcs. Egy csúcs 4 átlóegyenese közül a 3 egyenest 4-féleképpen, 6 összes egyenese közül pedig ‐ a II. a) számláláshoz hasonló meggondolással ‐ 6⋅5⋅4/6=20-féleképpen választhatjuk. Ezért az elfajulás 7⋅4, ill. 7⋅20 esetben áll be, a valóságos háromszögek száma 35⋅23-7⋅4=252, ill. 35⋅33-7⋅20=805.
2. Érdekes, hogy az egyenlő szárú háromszögek száma az a), b), c) esetek mindegyikében több, mint fele az összes háromszögeknek (az a) és c) esetekben pontosan 60%-a).