| Feladat: | 1045. matematika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bácsy Zs. , Biborka T. , Bollobás B. , Bónis Katalin , Fábián G. , Farkas Z. , Fejes L. , Fekete J. , Fritz J. , Gagyi Pálffy A. , Gálfi l. , Góth L. , Grüner Gy. , Hahn J. , Kardeván P. , Kóta G. , Kóta J. , Máté Zs. , Miklóssy E. , Molnár E. , Náray-Szabó G. , Nováky A. , Nováky B. , Pinkert A. , Sólyom I. , Szarka Gy. , Székely Jenő , Tattay Emőke , Várady G. , Zalán P. | ||
| Füzet: | 1961/április, 157 - 159. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gömbi geometria, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1960/május: 1045. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás: I. 1. A földfelszín egy pontjának az Egyenlítő síkjától, ill. a forgástengelytől való távolsága hosszúsági körének síkjában az sugárból és a szélességből , ill. (1. ábra felső része). 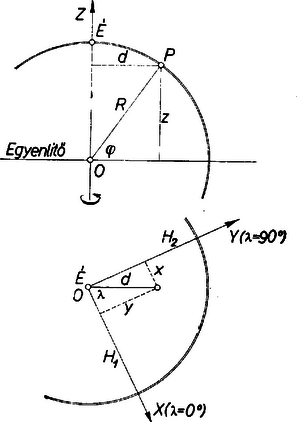 A Földet a szokásos állásban rajzolva és ennek megfelelően a déli szélességeket negatívnak véve is előjellel értendő. -re , ; -ra pedig , (minden távolságot km-ben adunk meg, így sehol sem lépünk túl a 4-jegyű táblázatokkal elérhető pontosságon). 2. A -os hosszúsági kör síkjától való távolság szélességi körének síkjában az előbbi -ből és a hosszúságból . (1. ábra alsó része). A nyugati hosszúságokat negatívnak véve, más szóval ha , is előjellel adódik. Hasonlóan a -os délkörök síkjától való távolság . -re , ; A-ra , . (A pontokat így tulajdonképpen egy az ábrázoló geometriából ismert, térbeli derékszögű koordinátarendszerben adtuk meg, ennek origója a Föld középpontja, -, -tengelye az Egyenlítő , ill. hosszúságú pontján lép ki (Accrától, ill. Kalkuttától délre), -tengelye pedig az Északi‐sarkon. 3. Eredményeinkből megkaphatjuk annak a téglatestnek az , , éleit, amelynek két csúcsa és , lapsíkjai pedig átmennek ezeken és párhuzamosak , , -vel; az élekből pedig folytatólag a húron mért távolságot, ugyanis a -nek testátlója. Éspedig , , , és így km. 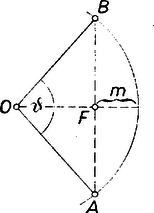 4. A Föld felszínén a legrövidebb ívet az sík metszi ki. A metszet főkör (2. ábra), így sugara . Legyen , ekkor az háromszögből a koszinusz tétellel Innen , ívmértékben , és így a felszínen mérve km. 5. Az húr legmélyebben, vagyis -hoz legközelebb fekvő pontja az felezőpont, mélysége km. II. A kívánt általános képletet a fentiek alapján adjuk meg, a szög kiszámítására. Ebből az ív egyszerűen megkapható. éleinek hossza ‐ esetleg ellentett előjellel, ez azonban a további négyzetreemelésre tekintettel nem lényeges: tehát
Megjegyzés. Általános eredményünk a gömbi trigonometria ún. oldal‐koszinusz tételének az ÉAB gömbháromszögre való alkalmazásával is megkapható, ahol É az Északi‐sark. Több dolgozat csak a végeredményre törekedve mindjárt ezt írta fel és ezt tekintette megoldásnak, ill. második megoldásnak. Itt a számpéldán felül annak beláttatása volt a cél, hogy a képlethez a gömbi trigonometria tételeinek rendszeres kiépítése nélkül is el lehet jutni. |