Kezdőlap


Feladat:	1044. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Góth László , Grüner György , Molnár Emil , Várady Gábor
Füzet:	1961/május, 212 - 214. oldal		PDF \| MathML
Témakör(ök):	Négyszögek geometriája, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1960/május: 1044. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Mindegyik oldal mindegyik átlóval együtt szerepel a négyszög egy-egy részháromszögében. A legrövidebb oldal, az $5$ cm-es és a hosszabb átló, a $13, 96$ cm-es csak olyan $p$ hosszúságú oldallal alkothat háromszöget, amelyre $5 + p > 13, 96$ , tehát $p > 8, 96$ . Ennek csak a $11$ cm-es oldal felel meg. A további két oldalra és erre az átlóra ugyancsak teljesül a háromszög-egyenlőtlenség:
$6 + 8 > 13, 96$ . Így csak olyan négyszög felelhet meg, amelyben az 5 és 11, (egyszersmind a 6 és 8) egységnyi oldalak szomszédosak.
Hasonlóan a $11$ cm-es oldal és a $4, 7$ cm-es átló csak olyan $q$ hosszúságú oldallal alkothat háromszöget, amelyre $q + 4, 7 > 11$ , azaz $q > 6, 3$ , így $q = 8$ , és a további két oldallal is teljesül $5 + 4, 7 > 6$ , ezért a $8$ és $11$ , valamint az $5$ és $6$ cm-es oldalpároknak is szomszédosaknak kell lenniük. ‐ Ezt az előbbivel egybevetve az $5$ cm-es oldal szomszédai a $11$ és $6$ cm-esek, tehát vele szemben a $8$ cm-es oldal fekszik. Így az oldalak sorrendje ‐ a legrövidebbel kezdve és valamelyik irányban haladva ‐ csak $5$ , $6$ , $8$ , $11$ lehet.
2. Nem biztos azonban, hogy a négyszög létezik, mert meghatározására 6, vagyis a szükségesnél 1-gyel több adatunk van. Meg kell tehát vizsgálnunk, hogy adataink együttese nem ellentmondásos-e. Ebben a függvénytáblázatokra vagyunk utalva, amelynek adatai kerekítettek. Ezért a négyszög létezését teljes biztonsággal nem állíthatjuk, de azt igen, hogy az adatok lehetnek-e egy létező négyszög adatainak jó közelítő értékei, vagy nem.
A megvizsgálásra egy lehetőség, hogy kétféleképpen számítjuk ki a négyszög szögeit ‐ ami úgyis feladatunk ‐ éspedig előbb az egyik, majd a másik átlóval való kettévágással keletkezett háromszögekből, és az eredményeket összehasonlítjuk. Vagyis az átlók egyikét, majd a másikát átmenetileg nem használjuk fel a számításban.
A szóban forgó $A B C D$ négyszög létezését feltételezve legyen $A B = 5$ , $B C = 6$ , $C D = 8$ , $D A = 11$ , $A C = 4, 7$ és $B D = 13, 96$ cm. Az $A C B$ és $A C D$ , valamint a $B D A$ és $B D C$ háromszögek szögei vagy a koszinusz-tétel, vagy az ún. félszög-képletek alapján számíthatók. A $B D C$ háromszögben mindenesetre az utóbbi látszik célszerűbbnek, ebben ugyanis két ,,kicsi'' hegyes és egy ,,nagy'' tompaszög van ‐ hiszen $B D$ alig kisebb a $B C + C D$ összegnél ‐, és várható, hogy ezek a táblázatgyűjteményben a $0^{\circ} - 5^{\circ}$ intervallumra sűrítetten közölt $lg sin$ -, ill. $lg tg$ -táblázat alapján pontosabban számíthatók; másrészt a koszinusz-függvény változása $0^{\circ}$ és $180^{\circ}$ közelében lassú, ilyen szögre a koszinusza alapján jóval tágabb korlátokat kapunk. A félszögek tangenséből számítunk, mert így csak $4$ szám logaritmusát kell kikeresnünk: a szokásos jelölésekkel az $s$ , $s - a$ , $s - b$ , $s - c$ számokét.
A $B D C$ háromszög $D$ és $B$ csúcsánál levő fél-szög tangensének és a $C$ -nél levő fél-szög kotangensének logaritmusára a

\begin{matrix} tg \frac{a}{2} = \sqrt[]{\frac{(s - b) (s - c)}{s (s - a)}} \end{matrix}

alakú képletekből a

\begin{matrix} 8, 5151 - 10, 8, 6404 - 10, 8, 8839 - 10 \end{matrix}

értékek adódnak, ezekből ¹ a fél-szögek értéke

\begin{matrix} 1, 875^{\circ}, 2, 502^{\circ}, 85, 623^{\circ}, \end{matrix}

tehát

B D C ∢ = 3, 75^{\circ}

D B C ∢ = 5, 00^{\circ}

B C D ∢ = 171, 25^{\circ}

. ‐ Másrészt a

B D A

háromszögből ugyanígy

B D A ∢ = 18, 72^{\circ}

D B A ∢ = 44, 90^{\circ}

B A D ∢ = 116, 38^{\circ}

. ‐ E két háromszögből közös oldaluk menti összeillesztéssel egyelőre két megoldásra kell gondolnunk, egy konvexre és egy konkávra.

Hasonlóan az

A C B

és az

A C D

háromszögből

\begin{matrix} B A C ∢ = 76, 34^{\circ}, B C A ∢ = 54, 08^{\circ}, A B C ∢ = 49, 58^{\circ}, \\ D A C ∢ = 40, 10^{\circ}, D C A ∢ = 117, 66, C D A ∢ = 22, 24^{\circ} . \end{matrix}

B

és

D

-nél most talált szögek nagyobbak az előbbi felbontás szerinti részeknél, tehát azokból a négyszög

B

és

D

szögeit összeadással kell képeznünk, ezért négyszögünk konvex, a csúcsoknál a két felbontásban talált szögek értéke rendre:

\begin{matrix} (B D -vel) D A B ∢ = 116, 38^{\circ}, A B C ∢ = 49, 90^{\circ}, B C D ∢ = 171, 25^{\circ}, C D A ∢ = 22, 47^{\circ} \\ (A C -vel) = 116, 44^{\circ}, = 49, 58^{\circ}, = 171, 74^{\circ}, = 22, 24^{\circ} . \end{matrix}

Az eltérések:

0, 06^{\circ}

0, 32^{\circ}

0, 49^{\circ}

és

0, 23^{\circ}

között vannak nagyobbak a kerekítések rovására írható hibáknál. ‐ Ha azonban pl. a

13, 96

cm-es átlót nem adatként tekintjük, hanem ismeretlenként a többi

5

adatból kiszámítjuk, arra jutunk, hogy a megoldást el kell fogadnunk. Ugyanis az

A C

átlóval való felbontásból nyert

A ∢ = 116, 44^{\circ}

és

C ∢ = 171, 74^{\circ}

szögekkel a

B D A

és

B D C

háromszögekből

\begin{matrix} B D^{2} = 25 + 121 - 110 \cdot (- 0, 4452) \approx 194, 97, \\ B D^{2} = 36 + 64 - 96 \cdot (- 0, 9896) \approx 195, 00, \end{matrix}

márpedig

13, 96^{2} = 194, 8816

és

13, 97^{2} = 195, 1609

, tehát a

B D^{2}

-re kapott értékek

4

értékes jegyre vett négyzetgyöke közelebb áll

13, 96

-hoz. ‐ Így viszont a szögeket csak

0, 1^{\circ}

-nyi pontossággal fogadhatjuk el:

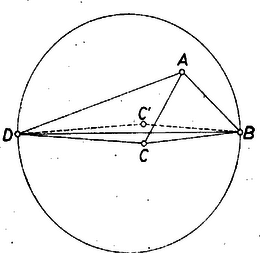
\begin{matrix} D A B ∢ = 116, 4^{\circ}, A B C ∢ = 49, 7^{\circ}, B C D ∢ = 171, 5^{\circ}, C D A ∢ = 22, 4^{\circ} . \end{matrix}

3. Egy a négyszöget lefedő kör átmérőjének legalább akkorának kell lennie, mint a két legtávolabbi csúcs távolsága. Itt erre a

B D

átló elegendő is, mert az

A

és

C

csúcsnál tompaszög van, tehát

A

és

C

belül vannak a

B D

átmérőjű Thalész-körön. Így a keresett sugár

6, 98

cm.

Összeállítva a következők dolgozataiból:

Góth László (Budapest, Könyves Kálmán g. II. o. t.),

Várady Gábor (Győr, Révai M. g. IV. o. t.),

Molnár Emil (Győr, Révai M. g. III. o. t.) és

Grüner György (Mosonmagyaróvár, Kossuth L. g. III. o. t.)

Megjegyzések. 1. A fenti 4 megoldás kivételével a dolgozatok nem vették figyelembe, hogy 1-gyel több adat van a kelleténél. Egy további dolgozat indokolás nélkül ezt mondta: ,,nincs a kívánalmaknak megfelelő négyszög''. ‐ A négyszög 4 szögét többnyire a

D A B

A B C

B C D

C D A

háromszögből számították, ‐ sőt gyakran csak 3-at ‐, és a

359, 45^{\circ}

-os szögösszegben mutatkozó hiányt ‐ ha egyáltalán észrevették ‐ kerekítési hibának tekintették.
2. Az adatokat pontosaknak tekintve az

A B C D

négyszög térbeli négyszög (torznégyszög), egyik csúcsa sincs benne a többi 3-mal meghatározott síkban, a többi 5 adathoz képest kissé rövidnek megadott

B D

átló a

B

és

D

csúcsot kissé összehúzza. Így

A B C D

-t tekinthetjük tetraédernek is. ‐ A tetraédert

6

éle egyértelműen meghatározza ‐ természetesen ha kapcsolódásuk rendje is adott. Ha már most a tetraéder egyik csúcsában összefutó 3 él

a

b

c

, a velük szemben fekvő élek pedig

a'

b'

c'

, akkor a tetraéder

V

térfogata determinánsok ¹ használatával így írható:

\begin{matrix} 288 V^{2} = | \begin{matrix} 2 a^{2} & a^{2} + b^{2} - c'^{2} & a^{2} + c^{2} - b'^{2} \\ b^{2} + a^{2} - c'^{2} & 2 b^{2} & b^{2} + c^{2} - a'^{2} \\ c^{2} + a^{2} - b'^{2} & c^{2} + b^{2} - a'^{2} & 2 c^{2} \end{matrix} | . \end{matrix}

Ha a 4 csúcs egy síkban van, akkor

V = 0

. Ebből adódik az ún. Euler-féle ,,négypontreláció:'' 4 pont akkor és csak akkor van egy síkban, ha a közülük kivehető

6

pontpár távolságaival ezen determináns értéke

0

. Adatainkból,

a = A B

b = A C

c = A D

, és így

a' = C D

b' = B D

c' = B C

-vel

V \approx 1, 603 {cm}^{3}

. Kiszámítva a lapok területét is, majd ezek alapján a tetraéder magasságait, kapjuk, hogy az

A

C

, ill.

B

D

csúcs távolsága a szemben levő laptól rendre közelítőleg

1

3

0, 2

, ill.

0, 3

0, 4

cm, kb. arányos a

B D

, ill.

A C

,,átlótól'' való távolsággal.

¹Ne felejtsük el a táblázat ,,

t

'' rovatában közölt kis módosítás figyelembevételét.

¹L. ide pl. Scharnitzky Viktor: A determinánsokról. K. M. L. 15 (1957) 33. és 75. o.