Kezdőlap


Feladat:	1043. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Fritz József , Nagy Dezső
Füzet:	1961/április, 155 - 157. oldal		PDF \| MathML
Témakör(ök):	Hiperbola egyenlete, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1960/május: 1043. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Helyezzünk az ábrára derékszögű koordinátarendszert, vegyük origónak $k$ középpontját, $X$ tengelynek a $d$ átmérő egyenesét. Legyen egy a követelménynek megfelelő kör $k'$ , és ennek középpontja 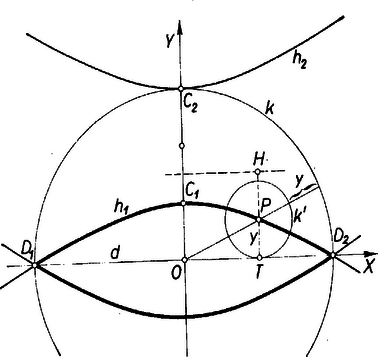$P (x, y)$ , továbbá $k$ sugara $r$ .

Nyilvánvaló, hogy

k

és

k'

-nek általában nincs közös pontja; mert ha van, akkor legrövidebb távolságuk és vele

k'

sugara 0, vagyis csak tágabb értelemben tekinthető körnek. Ilyenkor

k' \equiv P

, és ez a pont

k

-n is,

d

-n is rajta van, vagyis

d

-nek

D_{1}

D_{2}

végpontjai tágabb értelemben a mértani helyhez tartoznak. ‐ Minden más esetben

k'

és

d

(mint szakasz) érintkezési pontja, ami nyilván a

T (x, 0)

pont, a

k

belsejében van, és így egyrészt

\begin{matrix} - r \leq x \leq r, \end{matrix}

(1)

másrészt

k

magában foglalja

k'

-t, és így

P

-t is.
Szorítkozzunk egyelőre a mértani helynek az

y \geq 0

félsíkon levő pontjaira. Ekkor

k'

sugara, egyben

k

és

k'

legközelebbi pontjainak távolsága

y

P

-nek

k

-tól való távolsága

2 y

, és így

O P = r - 2 y

. (Ez pozitív, mert

k'

nem foglalhatja magában

O

-t ‐ különben ugyanis nem érinthetné

d

-t ‐, ezért

k'

-nek

k

-tól legtávolabbi pontja a

k

-nak ugyanazon a sugarán van, mint a

k

-hoz legközelebbi pontja, és így

\begin{matrix} r \geq 3 y . \end{matrix}

O P

-t a koordinátákkal is kifejezve, és két kifejezését összekapcsolva

\begin{matrix} \sqrt[]{x^{2} + y^{2}} = r - 2 y, \end{matrix}

innen négyzetreemeléssel és további átalakítással

\begin{matrix} 3 y^{2} - 4 r y - x^{2} + r^{2} = 0 \\ 3 {(y - \frac{2 r}{3})}^{2} - x^{2} = \frac{r^{2}}{3}, \end{matrix}

végül

\begin{matrix} \frac{{(y - \frac{2 r}{3})}^{2}}{{(\frac{r}{3})}^{2}} - \frac{x^{2}}{{(\frac{r}{\sqrt[]{3}})}^{2}} = 1. \end{matrix}

Ezek szerint minden (az

y \geq 0

félsíkon fekvő)

P

rajta van azon a hiperbolán, melynek középpontja a (0,

2 r / 3

) pont, valós tengelye az

Y

tengely, fő-, ill. melléktengelyének félhossza

r / 3

, ill.

r / \sqrt[]{3}

, és így csúcsai a

C_{1} (0, r / 3)

és a

C_{2} (0, r)

pontok.
Fordítva e hiperbolának nem minden pontja tartozik hozzá a keresett mértani helyhez. A

C_{2}

-t tartalmazó

h_{2}

ágnak nincs pontja

k

belsejében, mert az ág legkisebb ordinátájú pontja

C_{2}

, és ez éppen

k

-nak legnagyobb ordinátájú pontja; ‐ tehát

h_{2}

pontjai nem tartoznak a mértani helyhez.
A

C_{1}

-et tartalmazó

h_{1}

ág az

X

-tengelyt, mint az

y \geq 0

félsík határvonalát az

x = \pm r

abszcisszájú pontokban,

D_{1}

D_{2}

-ben metszi. Már most a

h_{1}

ág

D_{1} C_{1} D_{2}

ívének pontjai a

k

kör egyik félkörében vannak, rájuk az (1), az

y \geq 0

és a (2) feltételek mindegyike teljesül;

h_{1}

további pontjaira viszont nem.
Mindezek szerint a keresett mértani helyet a

D_{1} C_{1} D_{2}

hiperbolaív és ennek az

X

-tengelyre vett tükörképe alkotja.
Ha azokat a

P

-pontokat is elfogadjuk, amelyekkel

k'

d

szakasz meghosszabbításait érinti, akkor a

h_{1}

ág minden pontja a mértani helyhez tartozik. Ezekre ugyanis

y < 0

, így

k'

sugara

| y | = - y

, és mivel ekkor

k'

kívül van

k

-n, azért

O P = r + 2 | y | = r - 2 y

, vagyis teljesül a fenti követelmény. ‐ Viszont a

h_{2}

ágon azok a pontok vannak, amelyekre

O P = - (r - 2 y) = 2 y - r

, azaz

O P + r = 2 y

, vagyis amelyekre nézve

k

-nak

k'

-től legtávolabbi pontja annyira van

k'

-től, mint

k'

sugara.

Nagy Dezső (Budapest, Piarista g. III. o. t.)

Megjegyzés. Akik ismerik a hiperbolának ún. irányvonalas tulajdonságát, azok a 623. gyakorlat III. megoldásából¹ adódó

C C_{1} / H C_{1} = 2

megállapítás alapján is kimondhatják, hogy a mértani hely pontjai a fenti hiperbolán vannak. Könnyen meg lehet mutatni ugyanis, hogy az

{(x / a)}^{2} - {(y / b)}^{2} = 1

hiperbola minden pontjára az

F_{1} (c, 0)

fókusztól (ahol

c = \sqrt[]{a^{2} + b^{2}})

, és az

x = a^{2} / c

ún. irányvonaltól való távolságok aránya állandó, és értéke

c / a

, az ún. numerikus excentricitás, 1-nél nagyobb szám. (Ugyanez áll az

F_{2} (- c, 0)

és

x = - a^{2} / c

-től mért távolságokra.) Eszerint a szóban forgó hiperbola egyik fókusza a

k

kör középpontja, irányvonala a

d

-re merőleges sugár felező merőlegese és numerikus excentricitása 2.

Fritz József (Mosonmagyaróvár, Kossuth L. g. III. o. t.)

¹Lásd K. M. L. 22 (1961) 17. o.