Kezdőlap


Feladat:	1041. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bencsik I. , Biborka T. , Bollobás Béla , Bútor L. , Csikor F. , Farkas Z. , Fekete sJ. , Frint G. , Fritz J. , Gálfi l. , Góth L. , Grüner Gy. , Hahn J. , Kardeván P. , Kóta G. , Kóta J. , Máté Zsolt , Molnár E. , Náray-Szabó G. , Pribek F. , Simonovits M. , Sólyom István , Sonnevend Gy. , Székely J. , Várady G.
Füzet:	1961/május, 210 - 212. oldal		PDF \| MathML
Témakör(ök):	Számhármasok, Feladat
Hivatkozás(ok):	Feladatok: 1960/május: 1041. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. Sok megoldó helyesen állapította meg, hogy a feladat nem kívánja valamennyi szóban forgó számhármas előállítását. Az alábbi megoldások különböző előállításmódokat ismertetnek.

I. megoldás: Olyan számhármasokat adunk meg, amelyek négyzetgyökeivel mint oldalhosszakkal szerkesztett háromszög derékszögű. Legyenek a befogók

\sqrt[]{a_{1}}

és

\sqrt[]{a_{2}}

, ekkor Pythagorász tételével

a_{3} = a_{1} + a_{2}

, a

t

területre pedig

t = \sqrt[]{a_{1}} \cdot \sqrt[]{a_{2}} / 2

, és így a

a_{1} a_{2} = 4 t^{2}

. A két befogó egész, egymástól különböző, és nem teljes négyzet, ha pl.

a_{1} = 2

, és így

a_{2} = 2 t^{2}

, ahol

t

1

-nél nagyobb, tetszés szerinti egész szám; mert így

a_{2}

-nek törzsszám-szorzat alakú előállításában

2

kitevője páratlan szám (hiszen

t^{2}

-ben

2

kitevője páros). Ezekből

a_{3} = 2 (t^{2} + 1)

is egész,

a_{1}

és

a_{2}

-től különböző, és páros

t

esetén biztosan nem teljes négyzet, mert ekkor

t^{2}

is páros, tehát

a_{3}

egy páratlan szám

2

-szeresével egyenlő. Végül a

t = 2, 4, 6, ...

értékekkel képezett

\begin{matrix} a_{1} = 2, a_{2} = 2 t^{2}, a_{3} = 2 (t^{2} + 1) \end{matrix}

(1)

számhármasok közül bármely kettő lényegesen különböző, mert valamennyi számhármas az

a_{1} = 2

legkisebb tagban egyezik, a további két tagban pedig eltér egymástól.

Máté Zsolt (Szeged, Radnóti M. g. IV. o. t.)

Megjegyzés. Páratlan

t

-vel az

a_{3}

-ra adódó szám nem mindig teljesíti a 2. követelményt. Ugyanis

t = 2 q + 1

-gyel

a_{3} = 2 [{(2 q + 1)}^{2} + 1] = 4 [q^{2} + {(q + 1)}^{2}]

, és ez pl.

q = 3, 20, 119, 696

esetén teljes négyzet. A pythagorászi alap-számhármasokra ezen kötetünk 3. oldalának lábjegyzetében adott képletcsoport felhasználásával az 1009. feladat alapján végtelen sok ilyen

q

értéket lehet megadni.

II. megoldás: A 638. gyakorlatban látott elhelyezési bizonyítás megfordításával adunk megfelelő számhármasokat: tekintünk egy

c

d

egész oldalakkal bíró

A B C D

téglalapot, ennek

A B C

részháromszögében egy az oldalaktól

e

f

egész mértékszámú távolságra levő

E

pontot, és

a_{1}

a_{2}

a_{3}

gyanánt az

A E C

háromszög oldalainak négyzetét vesszük: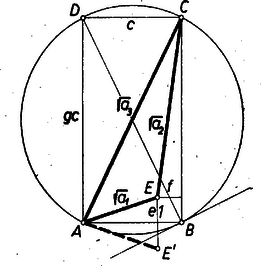

\begin{matrix} a_{1} = A E^{2} = {(c - f)}^{2} + e^{2}, a_{2} = E C^{2} = f^{2} + {(d - e)}^{2}, a_{3} = C A^{2} = c^{2} + d^{2} . \end{matrix}

Ezekkel

a_{1}

a_{2}

a_{3}

egészek és teljesül a 3. követelmény első része. Ezután

c

d

e

f

értékének megválasztására szóló előírásokkal biztosítjuk a további követelmények teljesülését.
Az 1. teljesül, ha pl.

d > c \geq 2

és

e = f = 1

, vagyis

a_{1} = {(c - 1)}^{2} + 1

a_{2} = {(d - 1)}^{2} + 1

; mert így

a_{1} < a_{2}

, és mindkettő kisebb az

A C

átló négyzeténél,

a_{3}

-nál. Egyszersmind

a_{1}

és

a_{2}

-re 2. is teljesül, mert pozitív egész szám négyzetét

1

-gyel növelve nem kaphatunk négyzetszámot. Hasonlóan

a_{3}

sem teljes négyzet, ha pl.

d = g c

, ahol

g

1

-nél nagyobb egész szám, mert így

a_{3} = c^{2} (1 + g^{2})

, és itt

1 + g^{2}

nem teljes négyzet. Végül az

A C E

háromszög

t

területe

\begin{matrix} t = t_{A B C} - t_{A B E} - t_{B C E} = \frac{c d}{2} - \frac{c}{2} - \frac{d}{2} = \frac{1}{2} [(c - 1) (d - 1) - 1] = \\ = \frac{1}{2} [(c - 1) (g c - 1) - 1], \end{matrix}

és ennek egész voltához szükséges és elegendő, hogy

c - 1

és

g c - 1

páratlan legyen, vagyis, hogy

c

páros legyen.
Most már állandó

g

-vel és

c = 2, 4, 6, 8, ...

mellett a

\begin{matrix} a_{1} = {(c - 1)}^{2} + 1, a_{2} = {(g c - 1)}^{2} + 1, a_{3} = (1 + g^{2}) c^{2} \end{matrix}

(2)

képlethármas tetszés szerinti számú, a feltételeknek megfelelő számhármast ad. Ezek egymástól lényegesen különbözők, mert

a_{1} < a_{2} < a_{3}

folytán a

c

-től különböző

c'

értékhez tartozó

a'_{1}

a'_{2}

a'_{3}

számhármas csak akkor volna szorzással előállítható

a_{1}

a_{2}

a_{3}

,-ból, ha állna

a'_{3} : a_{3} = a'_{2} : a_{2}

, márpedig az innen adódó

a'_{3} a_{2} - a_{3} a'_{2} = 0

-ból behelyettesítéssel és rendezéssel

\begin{matrix} (c - c') [(g - 1) c c' + (c - 1) (c' - 1) - 1] \end{matrix}

ez pedig lehetetlen, mert egyik tényező sem 0 (a második biztosan pozitív).

Sólyom István (Budapest, Vörösmarty M. g. III. o. t.)

Megjegyzések. 1. Négyzetből kiindulva is kaphatunk megoldást, ha ennek oldala

2 c

(> 4)

és

E

-t az oldalaktól

1

, ill.

3

egységnyi távolságban vesszük.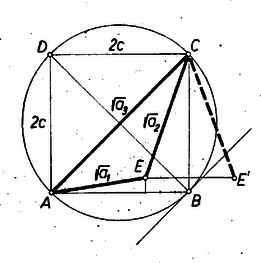

Ekkor

\begin{matrix} a_{1} = {(2 c - 3)}^{2} + 1, a_{2} = {(2 c - 1)}^{2} + 9, a_{3} = 8 c^{2} . \end{matrix}

(3)

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

2. A (2) és (3) számhármasokhoz tartozó háromszögek mindegyike

E

-nél tompaszögű, mert

E

benne van az

A B C

háromszögben, tehát az

A C

átmérő fölött

k

Thalész-körben is. Ha azonban

E

-t (2) esetén az

A B

, (3) esetén a

B C

-re való

E'

tükörképével cseréljük ki, akkor az

A C E'

háromszög hegyesszögű, mert

E'

k

-hoz

B

-ben húzott érintőnek

k

-val ellentétes oldalán van. E cserékkel

\begin{matrix} a_{1} = {(c - 1)}^{2} + 1, a_{2} = {(g c + 1)}^{2} + 1, a_{3} = (1 + g^{2}) c^{2}; & (2') \\ a_{1} = {(2 c + 3)}^{2} + 1, a_{2} = {(2 c - 1)}^{2} + 9, a_{3} = 8 c^{2} . & (3') \end{matrix}

E számhármasok tagjai is különbözők, (

2'

)-ben

a_{2} ≶ a_{3}

(

3'

)-ban

a_{1} ≶ a_{3}

, mert az

a_{2} = a_{3}

, ill.

a_{1} = a_{3}

egyenlőség feltevése

c

-re a

c^{2} - 2 g c - 2 = 0

, ill.

2 c^{2} - 6 c - 5 = 0

egyenletre vezet, diszkriminánsuk

4 (g^{2} + 2)

, ill.

76

, nem teljes négyzet, tehát így

c

nem lehetne racionális.