Feladat: 1040. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bencsik I. ,  Biborka Tamás ,  Bollobás Béla ,  Farkas Z. ,  Fekete J. ,  Frint G. ,  Fritz József ,  Gálfi László ,  Grüner Gy. ,  Kóta G. ,  Kóta József ,  Krámli A. ,  Máté Attila ,  Meleghegyi L. ,  Molnár E. ,  Nagypál Botond ,  Náray-Szabó G. ,  Pinkert A. ,  Simonovits M. ,  Szegő K. ,  Székely J. ,  Tattay Emőke ,  Várady G. 
Füzet: 1961/május, 206 - 210. oldal  PDF  |  MathML 
Témakör(ök): Négyzetrács geometriája, Teljes indukció módszere, Feladat
Hivatkozás(ok):Feladatok: 1960/május: 1040. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: 1. A 971. feladatban* bebizonyítottuk, hogy a K(2,1/3) pont körül írt bármely körön legfeljebb egy rácspont van, más szóval, hogy nincs két olyan rácspont, amely K-tól egyenlő távol volna. A 971. feladat állítása és bizonyítása érvényes minden olyan K pontra, melynek egyik koordinátája irracionális, a másik pedig olyan racionális szám, melynek tovább nem egyszerűsíthető alakjában a nevező legalább 3. Mi a további meggondolásokat a fenti K pontra fogjuk alkalmazni.
A sík rácspontjainak K-tól mért távolságai úgy rendezhetők nagyság szerint növekvő sorozatba, hogy a sorozat bármely két tagja különböző. Jelöljük az n-edik távolságot a sorozatban rn-nel. Ha K körül olyan r sugárral írunk k kört, amelyre rn<r≤rn+1, akkor k belsejében pontosan n rácspont van, mindazok, amelyeknek K-tól mért távolsága r1,r2,...,rn. Minden más rácspont vagy k-n kívül, vagy k kerületén van (ha 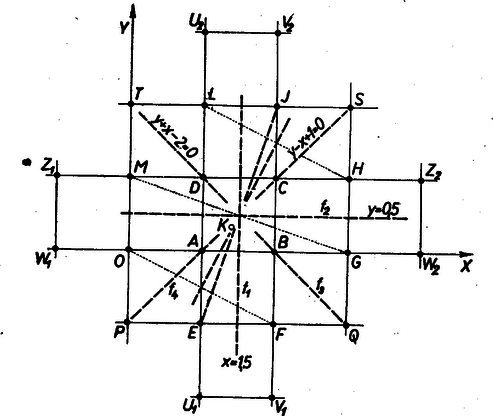r=rn+1).

 
 
1. ábra
 

2. Alkalmazzuk a fentieket K(2,1/3) és n=10 mellett. Előkészítésül tekintsük K távolságát a K-t magába foglaló ABCD=N1 egységnyi rácsnégyzet csúcsaitól (1. ábra), e négyzet oldalai az x=1, x=2, y=0 és y=1 egyenesek. A távolságok nagyságviszonyát megállapíthatjuk kiszámításuk nélkül is. Éspedig KA<KB és KD<KC, mert K az AB és DC szakaszok közös f1 felező merőlegesének, vagyis az x=1,5 egyenesnek azon az oldalán van, mint A és D, ugyanis K abszcisszájára 2<1,5. Hasonlóan AD-nek f2 felező merőlegese alapján KA<KD és KB<KC, továbbá BD-nek f4 felező merőlegese alapján KB<KD, ugyanis f4 egyenlete: y-x+1=0, és itt a bal oldal K-ra a B-vel egyenlő jelű: 4/3-2<0 és -1<0, másrészt ellentett jelű, mint D-re: 1>0. Ezek szerint KA<KB<KD<KC.
Áttérve az N1-et magábafoglaló PQST=N2 rácsnégyzet csúcsaiban és oldalszakaszain fekvő rácspontokra, egyrészt az előzőkhöz hasonlóan KP<KQ<KT<KS, ‐ másrészt az AC szakasz f3 felező merőlegesét (y+x-2=0) is felhasználva ‐ rendre f1, f3, f2 és f4 alapján KE<KF<KG<KH<KJ, továbbá f4, f2, f3 és f1 alapján KE<KO<KM<KL<KJ. Eszerint az EFGHJLMO=N3 nyolcszög csúcsai közül E van K-hoz legközelebb, J legtávolabb.
Nyilvánvaló, hogy az N3 csúcsaitól egységnyi távolságra levő, az N1 és N2 csúcsaitól különböző U1,V1,W2,...,Z1,W1 rácspontok vizsgálata után minden más rácsponttól eltekinthetünk, mert K-tól távolabb vannak, mint a már figyelembe vettek. E 8 pont közül az eddigiekhez hasonlóan U1 van legközelebb K-hoz, de PU1 felező merőlegese (y-x+2=0) alapján KU1>KP.
Mármost EC felező merőlegese (2y+x-1,5=0) alapján KC<KE és PJ felező merőlegese (3y+2x-3,5=0) alapján KJ<KP, tehát a K-hoz legközelebbi 4 rácspont N1 négy csúcsa, a következő 8 pedig N3 nyolc csúcsa, továbbá r12=KJ. Mivel még f1, alapján KM<KH, azért KL és KH kisebbike adja r10-et, nagyobbika r11-et. LH felező merőlegese (y-2x+2,5=0) alapján KL<KH, tehát L-nek a keresett körben kell lennie, H-nak pedig rajta kívül, vagy a kerületén. Így a keresett kör sugarára
KL=r10=1352-182<r≤13103-542=r11=KH,
azaz közelítőleg 1,717<r<1,721.
 

Gálfi László (Budapest, Fazekas M. gyak. g. II. o. t.)
Kóta József (Tatabánya, Árpád g. II. o. t.) és
Máté Attila (Szeged, Dózsa Gy. ált. isk. VII. o. t.)
 

II. megoldás: 1. Az állítást (a 971. feladat eredményére nem támaszkodva) a teljes indukció módszerével bizonyítjuk. Az origó körül r=1/2 (vagy bármely 0<r<1) sugárral írt kör belsejében pontosan egy rácspont van, maga a kezdőpont. A K(1/2,0), körül r=1 (vagy bármely 1/2<r≤5/2) sugárral írt kör belsejében pontosan két rácspont van: az origó és az (1,0) pont; tehát az állítás n=1 és n=2-re igaz.
Feltesszük, hogy van olyan K1 pont és ehhez olyan r, sugár, hogy a K1, körül r1 sugárral írt k1 kör belsejében pontosan n-1 (≥1) rácspont van, és megmutatjuk, hogy ekkor van olyan kör, melynek belsejében pontosan n rácspont van.
Tekintsük azon rácspontok k1-től való d távolságát, amelyek nincsenek k1 belsejében (d-t a P pontra nyilvánvalóan a K1P szakasznak k1-en kívül eső K1P-r1 szakasza adja meg). E távolságok között nyilván vagy egy, vagy több legkisebb van (vagyis olyan, amelynél nincs kisebb).
a) Ha csak egy d1 legkisebb távolság van, és ez a P ponthoz tartozik, akkor ezt figyelmen kívül hagyva ismét van olyan távolság, amelynél nincs kisebb, legyen ez d2. Ekkor a K1 körül r1+d2 sugárral írt kör belsejében benne van a korábbi n-1 rácspont és P, azaz pontosan n rácspont. Ezt akartuk bizonyítani.
b) Ha több olyan távolság van, amelynél nincs kisebb, és ezek a P1,P2,...,Pi rácspontokhoz tartoznak, akkor e pontok vagy a k1-en kívül vannak, egy a k1-gyel koncentrikus ki kör kerületén, vagy a k1 kerületén. Az utóbbi esetben k1 helyett kijelölhetünk olyan vele koncentrikus és kisebb sugarú k1* kört, mely a k1-beli n-1 rácspontot ugyancsak a belsejében tartalmazza, és amelynek a kerületén egyetlen rácspont sincs. Vegyük evégett a k1 belsejében levő rácspontok közül a K1-től legtávolabbit, vagy ha több ilyen van, akkor bármelyiküket, legyen az Q, és ekkor k1* gyanánt nyilvánvalóan megfelel az (r1+K1Q)/2 sugarú kör. Eszerint elegendő arra az esetre végeznünk a bizonyítást, ha a P1,P2,...,Pi pontok nincsenek k1 kerületén.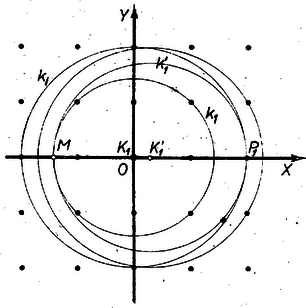
 
 
2. ábra
 

Ezt az esetet k1 helyett egy alkalmas k1' kör, kijelölésével visszavezethetjük az a) esetre. Legyen k1 és a P1K1 egyenes P1-től távolabbi metszéspontja M, ekkor k1' a P1M átmérőjű kör. Ez valóban megfelel az a) eset feltételeinek, mert 1) magában foglalja k1-et és az annak belsejében levő n-1 rácspontot; 2) további rácspontot nem tartalmaz, mert benne fekszik ki-ben, márpedig ki belsejében nincs más rácspont, mint a k1-beliek; végül 3) ki-vel egyetlen közös pontja P1, tehát P1 kisebb távolságra van k1'-től, mint P2,P3,...,Pi bármelyike.
Ezzel a bizonyítást befejeztük.
2. Az előírt K és r megadásában a fentiektől kissé eltérünk: kiindulási k1 körünk belsejében és a kerületén együttvéve 10-1=9 rácspont lesz; látni fogjuk azonban, hegy ez az eltérés a továbbiakban nem lényeges. ‐ Legyen k1 az origó körüli 2 sugarú kör. Ebben benne vannak a (0,0), (±1,0) és (0,±1) pontok és a kerülelén a (±1,±1) pontok. Itt a fenti b) esettel állunk szemben, k1-höz legközelebb a (2,0), (0,2), (-2,0) és (0,-2) pontok vannak. Vegyük P1-nek (2,0)-t, ekkor a fenti M pont: (-2,0), k1' középpontja K1' (1-12,0), sugara pedig 1+12. Egyszerű számítás mutatja, hogy k1'-höz kívülről legközelebb a (2,±1) pontok vannak, ezek alapján a feladat 2. részének egy megoldása a
K1'(1-12,0)pont és1+12<r≤(1+12)2+1.

A k1-en és a kerületén levő 9 rácspont a k1' belsejében van, mert k1 és k1' egyetlen közös pontja M, és ez nem rácspont. Egyébként a megadott korlátok közti r-rel körünk k1'-t is magában foglalja.
 

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.) és

Biborka Tamás (Makó, József A. g. III. o. t.)
 

Megjegyzések. 1. Nem kell azt gondolnunk, hogy racionális koordinátákkal bíró pont nem felelhet meg K gyanánt. Tekintsük az origó körüli 2 egységnyi sugarú kört, ennek belsejében 9, a kerületén 4 rácspont van, és toljuk el a középpontját a (0,1/4) pontba. Így 3 kerületi rácspont külső ponttá, 1 pedig belsővé válik, megoldást kaptunk; itt 49<16r2≤65.
 

Fritz József (Mosonmagyaróvár, Kossuth L. g. III. o. t.)
 

2. Hasonlóan K (1/3,0) és 25<9r2≤34 is megoldás.
 

Nagypál Botond (Orosháza, Táncsics M. g. III. o. t.)
 

3. Néhány érdekes eredmény a dolgozatok számpéldáiból: Az r korlátai közti különbség az I. megoldásban a legkisebb, ‐ legnagyobb viszont a 2. megjegyzésben. ‐ A két korláttal szerkesztett ,,üres'' körgyűrű területe 3 megoldásban is π, éspedig a II. megoldásban és a két megjegyzésben; ennél nagyobb területű körgyűrű nem fordult elő. ‐ r alsó korlátjára a legkisebb előfordult érték: K (1/2,1/3) mellett Máté Zsoltnál: 97<36r2. (Még kisebb alsó korlát is adható volna az egységnyi rácsnégyzet középpontjához közel választott K-val.) ‐ A felső korlát legnagyobb előfordult értéke az 1. megjegyzésbeli eredményhez tartozik.
4. Nem nehéz belátni, hogy növekvő n esetén a belsejükben pontosan n rácspontot tartalmazó különböző körök sugara egyre szűkebb korlátok közé szorul és közelítőleg az n/π hányados négyzetgyökével egyenlő.
*Lásd K. M. L. 20 (1960) 24. o.